
分析 由{bn}的前n项和为Sn=$\frac{3}{2}$(3n-1)求得bn,进一步得到an,把an,bn代入λan>bn+36(n-3)+3λ,分离λ,然后求出关于n的函数的最大值得答案.
解答 解:由Sn=$\frac{3}{2}$(3n-1),得${b}_{1}={S}_{1}=\frac{3}{2}(3-1)=3$,
当n≥2时,${b}_{n}={S}_{n}-{S}_{n-1}=\frac{3}{2}({3}^{n}-1)-\frac{3}{2}({3}^{n-1}-1)={3}^{n}$,
当n=1时,上式成立,∴${b}_{n}={3}^{n}$.
代入an=2bn+3,得${a}_{n}=2•{3}^{n}+3$,
代入λan>bn+36(n-3)+3λ,得λ(an-3)>bn+36(n-3),
即2λ•3n>3n+36(n-3),
则λ>$\frac{1}{2}$+$\frac{18(n-3)}{{3}^{n}}$.
由$\frac{18(n-2)}{{3}^{n+1}}-\frac{18(n-3)}{{3}^{n}}$=$\frac{126-36n}{{3}^{n+1}}>0$,得n≤3.
∴n=4时,$\frac{1}{2}$+$\frac{18(n-3)}{{3}^{n}}$有最大值为$\frac{13}{18}$.
故答案为:($\frac{13}{18}$,+∞).
点评 本题考查数列递推式,考查了数列的函数特性,训练了恒成立问题的求解方法,是中档题.


科目:高中数学 来源: 题型:解答题
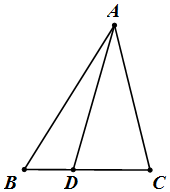 在△ABC中,D为BC边上的动点,且AD=3,B=$\frac{π}{3}$.
在△ABC中,D为BC边上的动点,且AD=3,B=$\frac{π}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{19}{25}$ | B. | $\frac{25}{36}$ | C. | $\frac{31}{48}$ | D. | $\frac{49}{64}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -15 | B. | $-\frac{1}{2}$ | C. | -11 | D. | $-\frac{31}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com