
分析 (1)由函数f(x)=ax+b(a>0且a≠1)的图象经过点(2,0),(0,-2),可得$\left\{\begin{array}{l}{a}^{2}+b=0\\ 1+b=-2\end{array}\right.$,解得a和b的值;
(2)由(1)得f(x)=$\sqrt{3}$x-3,当x∈[2,4]时,函数y=f(x)为增函数,进而可得函数的最值.
解答 解:(1)∵函数f(x)=ax+b(a>0且a≠1)的图象经过点(2,0),(0,-2).
∴$\left\{\begin{array}{l}{a}^{2}+b=0\\ 1+b=-2\end{array}\right.$,
解得:$\left\{\begin{array}{l}a=\sqrt{3}\\ b=-3\end{array}\right.$,
(2)由(1)得f(x)=$\sqrt{3}$x-3,
当x∈[2,4]时,函数y=f(x)为增函数,
故当x=2时,函数y=f(x)的最小值为0,
当x=4时,函数y=f(x)的最大值为6.
点评 本题考查的知识点是函数的最值及其几何意义,函数解析式的求法,难度基础.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | N>M>K | B. | K>M>N | C. | M>K>N | D. | M>N>K |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $?{x_0}∈R,{2^{{x_0}-1}}≥1$ | B. | $?{x_0}∈R,{2^{{x_0}-1}}>1$ | ||
| C. | ?x∈R,2x-1≤1 | D. | ?x∈R,2x-1>1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
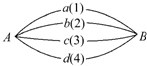 如图,从A地到B地设置了4条不同的网络线路,它们通过的最大信息量分别为1,2,3,4,现从中任取三条网线连通A,B两地(三条网线可通过的信息总量即三条网线各自的最大信息量之和).
如图,从A地到B地设置了4条不同的网络线路,它们通过的最大信息量分别为1,2,3,4,现从中任取三条网线连通A,B两地(三条网线可通过的信息总量即三条网线各自的最大信息量之和).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
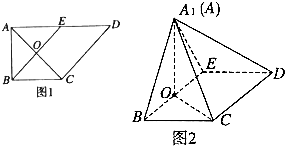 如图1,在直角梯形ABCD中,AD∥BC,∠BAD=90°,AB=BC=1,AD=2,E是AD的中点,O是AC与BE的交点.将△ABE沿BE折起到△A1BE的位置,如图2.
如图1,在直角梯形ABCD中,AD∥BC,∠BAD=90°,AB=BC=1,AD=2,E是AD的中点,O是AC与BE的交点.将△ABE沿BE折起到△A1BE的位置,如图2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com