
【题目】判断下列命题是否正确,请说明理由:
(1)若向量![]() 与
与![]() 同向,且
同向,且![]() ,则
,则![]() ;
;
(2)若向![]() ,则
,则![]() 与
与![]() 的长度相等且方向相同或相反;
的长度相等且方向相同或相反;
(3)对于任意向量![]() ,若
,若![]() 与
与![]() 的方向相同,则
的方向相同,则![]() =
=![]() ;
;
(4)由于![]() 方向不确定,故
方向不确定,故![]() 不与任意向量平行;
不与任意向量平行;
(5)向量![]() 与
与![]() 平行,则向量
平行,则向量![]() 与
与![]() 方向相同或相反.
方向相同或相反.
【答案】(1)不正确,理由见解析 (2)不正确,理由见解析(3)正确,理由见解析 (4)不正确,理由见解析 (5) 不正确,理由见解析
【解析】
(1)根据平面向量的定义判断.(2)![]() 只能判断两向量长度相等,方向不确定.(3)根据平面向量的定义判断.(4)规定:
只能判断两向量长度相等,方向不确定.(3)根据平面向量的定义判断.(4)规定:![]() 与任意向量平行(5)考虑零向量的情况.
与任意向量平行(5)考虑零向量的情况.
(1)不正确.因为向量由两个因素来确定,即大小和方向,所以两个向量不能比较大小.
(2)不正确.由|![]() 只能判断两向量长度相等,不能确定它们的方向关系.
只能判断两向量长度相等,不能确定它们的方向关系.
(3)正确.因为|![]() ,且
,且![]() 与
与![]() 同向,由两向量相等的条件,可得
同向,由两向量相等的条件,可得![]() =
=![]()
(4)不正确.依据规定:![]() 与任意向量平行.
与任意向量平行.
(5)不正确.因为向量![]() 与
与![]() 若有一个是零向量,则其方向不定.
若有一个是零向量,则其方向不定.


 步步高达标卷系列答案
步步高达标卷系列答案科目:高中数学 来源: 题型:
【题目】已知数列{an}满足:an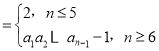 (n∈N*).若正整数k(k≥5)使得a12+a22+…+ak2=a1a2…ak成立,则k=( )
(n∈N*).若正整数k(k≥5)使得a12+a22+…+ak2=a1a2…ak成立,则k=( )
A.16B.17C.18D.19
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于数列![]() ,若
,若![]() ,则称数列
,则称数列![]() 为“广义递增数列”,若
为“广义递增数列”,若![]() ,则称数列
,则称数列![]() 为“广义递减数列”,否则称数列
为“广义递减数列”,否则称数列![]() 为“摆动数列”.已知数列
为“摆动数列”.已知数列![]() 共4项,且
共4项,且![]() ,则数列
,则数列![]() 是摆动数列的概率为______.
是摆动数列的概率为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着“互联网+交通”模式的迅猛发展,“共享自行车”在很多城市相继出现。某运营公司为了了解某地区用户对其所提供的服务的满意度,随机调查了40个用户,得到用户的满意度评分如下:
用户编号 | 评分 | 用户编号 | 评分 | 用户编号 | 评分 | 用户编号 | 评分 | |||
1 2 3 4 5 6 7 8 9 10 | 78 73 81 92 95 85 79 84 63 86 | 11 12 13 14 15 16 17 18 19 20 | 88 86 95 76 97 78 88 82 76 89 | 21 22 23 24 25 26 27 28 29 30 | 79 83 72 74 91 66 80 83 74 82 | 31 32 33 34 35 36 37 38 39 40 | 93 78 75 81 84 77 81 76 85 89 |
用系统抽样法从40名用户中抽取容量为10的样本,且在第一分段里随机抽到的评分数据为92.
(1)请你列出抽到的10个样本的评分数据;
(2)计算所抽到的10个样本的均值![]() 和方差
和方差![]() ;
;
(3)在(2)条件下,若用户的满意度评分在![]() 之间,则满意度等级为“
之间,则满意度等级为“![]() 级”。试应用样本估计总体的思想,根据所抽到的10个样本,估计该地区满意度等级为“
级”。试应用样本估计总体的思想,根据所抽到的10个样本,估计该地区满意度等级为“![]() 级”的用户所占的百分比是多少?
级”的用户所占的百分比是多少?
(参考数据:![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平行六面体ABCD-A1B1C1D1中,AA1⊥平面ABCD,且AB=AD=2,AA1=![]() ,∠BAD=120°.
,∠BAD=120°.
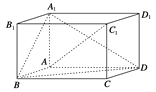
(1)求异面直线A1B与AC1所成角的余弦值;
(2)求二面角B-A1D-A的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 。
。
(1)当![]() 时,求函数
时,求函数![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)若函数![]() ,讨论函数
,讨论函数![]() 的单调性;
的单调性;
(3)若(2)中函数![]() 有两个极值点
有两个极值点![]()
![]() ,且不等式
,且不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com