
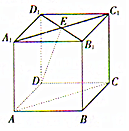
 如图所示,在正方体AC1中,AB=2,A1C1∩B1D1=E,直线AC与直线DE所成的角为α,直线DE与平面BCC1B1所成的角为β,则cos(α-β)=( )
如图所示,在正方体AC1中,AB=2,A1C1∩B1D1=E,直线AC与直线DE所成的角为α,直线DE与平面BCC1B1所成的角为β,则cos(α-β)=( )| A. | $\frac{\sqrt{6}}{6}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{30}}{6}$ | D. | $\frac{\sqrt{6}}{3}$ |
分析 连接BD交AC于O,连接OB1,过O作OM⊥BC于M,连接B1M,B1A,B1C.求出α=90°,证明OM⊥平面BCC1B1,得出cos(α-β)=sinβ=$\frac{OM}{O{B}_{1}}$.
解答 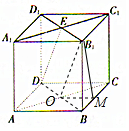 解:连接BD交AC于O,连接OB1,过O作OM⊥BC于M,连接B1M,B1A,B1C.
解:连接BD交AC于O,连接OB1,过O作OM⊥BC于M,连接B1M,B1A,B1C.
∵B1A=B1C,O是AC的中点,∴OB1⊥AC,
∵B1E$\stackrel{∥}{=}$OB,∴四边形ODEB1是平行四边形,
∴OB1∥DE,
∴DE⊥AC,
∴直线AC与直线DE所成的角为α=90°,
∵OM⊥BC,OM⊥BB1,
∴OM⊥平面BCC1B1,
∴∠OB1M为直线DE与平面BCC1B1所成的角β,
∴cos(α-β)=sinβ=$\frac{OM}{O{B}_{1}}$,
∵正方体的棱长AB=2,∴OM=1,OB=$\frac{1}{2}BD$=$\sqrt{2}$,
∴OB1=$\sqrt{4+2}$=$\sqrt{6}$,
∴sinβ=$\frac{1}{\sqrt{6}}$=$\frac{\sqrt{6}}{6}$.
故选A.
点评 本题考查了空间角的计算,作出要求的空间角是解题的关键,也可用向量法求出α,β,再计算cos(α-β),属于中档题.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:高中数学 来源: 题型:解答题
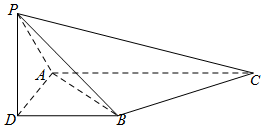 如图,三棱锥P-ABC,侧棱PA=2,底面三角形ABC为正三角形,边长为2,顶点P在平面ABC上的射影为D,有AD⊥DB,且DB=1.
如图,三棱锥P-ABC,侧棱PA=2,底面三角形ABC为正三角形,边长为2,顶点P在平面ABC上的射影为D,有AD⊥DB,且DB=1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
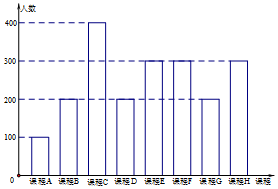 为了响应教育部颁布的《关于推进中小学生研学旅行的意见》,某校计划开设八门研学旅行课程,并对全校学生的选课意向进行调查(调查要求全员参与,每个学生必须从八门课程中选出唯一一门课程).本次调查结果如下.图中,课程A,B,C,D,E为人文类课程,课程F,G,H为自然科学类课程.为进一步研究学生选课意向,结合上面图表,采取分层抽样方法从全校抽取1%的学生作为研究样本组(以下简称“组M”).
为了响应教育部颁布的《关于推进中小学生研学旅行的意见》,某校计划开设八门研学旅行课程,并对全校学生的选课意向进行调查(调查要求全员参与,每个学生必须从八门课程中选出唯一一门课程).本次调查结果如下.图中,课程A,B,C,D,E为人文类课程,课程F,G,H为自然科学类课程.为进一步研究学生选课意向,结合上面图表,采取分层抽样方法从全校抽取1%的学生作为研究样本组(以下简称“组M”).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{e^2}{2}$ | B. | $\frac{{3{e^2}}}{2}$ | C. | $\frac{e^2}{4}$ | D. | $\frac{e^2}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 2 | C. | -3 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com