Question

1．若曲线x²+y²=5与曲线x²+y²-2mx+m²-20=0（m∈R）相交于A，B两点，且两曲线A处的切线互相垂直，则m的值是±5．

Answer 1

分析 由题意画出已知两个圆的图象，利用圆的性质可以得到两切线互相垂直时应该过对方的圆心，O₁A⊥AO₂，由勾股定理可得m的值．

解答 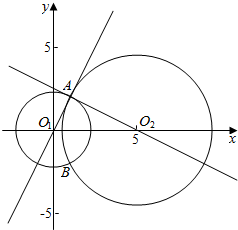解：由题知圆O₁（0，0），O₂（m，0），
x²+y²-2mx+m²-20=0即为（x-m）²+y²=20，
半径分别为$\sqrt{5}$，2$\sqrt{5}$，
根据两圆相交，
可得圆心距大于两圆的半径之差而小于半径之和，
即$\sqrt{5}$＜|m|＜3$\sqrt{5}$，
又O₁A⊥O₂A，所以有 m²=（$\sqrt{5}$）²+（2$\sqrt{5}$）²=25，
∴m=±5．
故答案为：±5．

点评 本题主要考查圆的标准方程、两直线的位置关系、直线和圆相切的性质等知识，属于中档题．