
| A. | y=$\sqrt{2}$x+2 | B. | y=-$\sqrt{2}$x+2 | C. | y=$\sqrt{2}$x+2或y=-$\sqrt{2}$x-2 | D. | y=$\sqrt{2}$x+2或y=-$\sqrt{2}$x+2 |
分析 设直线方程为:y=kx+2,将直线方程代入双曲线方程,结合韦达定理求出|EF|,再利用点到直线的距离公式求出原点O到直线的距离d,根据S=$\frac{1}{2}$×|EF|×d=$2\sqrt{2}$,求得k值,并验证△>0.
解答 解:由题意得:直线l的斜率一定存在,设l:y=kx+2,
由$\left\{\begin{array}{l}{y=kx+2}\\{{x}^{2}{+y}^{2}=2}\end{array}\right.$⇒(1-k2)x2-4kx-6=0,△=16k2+24(1-k2)=24-8k2
则$\left\{\begin{array}{l}{1{-k}^{2}≠0}\\{△>0}\end{array}\right.$⇒k2<3且k≠±1,
x1+x2=$\frac{4k}{1{-k}^{2}}$,x1x2=-$\frac{6}{1{-k}^{2}}$,|EF|2=(1+k2)[${{(x}_{1}{+x}_{2})}^{2}$-4x1x2]=(1+k2)$\frac{24-{8k}^{2}}{{(1{-k}^{2})}^{2}}$,
∵原点到直线的距离d=$\frac{2}{\sqrt{1{+k}^{2}}}$,
S△=$\frac{1}{2}$×|EF|×d=$\frac{1}{2}$×$\sqrt{(1{+k}^{2})\frac{24-{8k}^{2}}{{(1-k)}^{2}}}$×$\frac{2}{\sqrt{1{+k}^{2}}}$=2$\sqrt{2}$⇒k4-k2-2=0,
解得k2=2或k2=-1(舍去),即k=±$\sqrt{2}$,
故所求直线方程为$\sqrt{2}$x-y+2=0或$\sqrt{2}$x+y-2=0.
即y=$\sqrt{2}$x+2或y=-$\sqrt{2}$x+2,
故选:D
点评 本题考查了直线与双曲线的关系,韦达定理,点到直线的距离公式,考查了学生的运算能力,综合性强.解答本题一定要注意验证△>0.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{7}$ | B. | $\frac{3}{7}$ | C. | $\frac{5}{7}$ | D. | $\frac{4}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{5}$ | B. | $\frac{1}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{7}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{245}{128}$ | B. | $\frac{509}{256}$ | C. | $\frac{1003}{512}$ | D. | $\frac{2013}{1024}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4个 | B. | 7个 | C. | 8个 | D. | 16个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
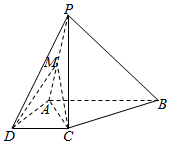 如图,在四棱锥P一ABCD中,PC=AD=CD=$\frac{1}{2}$AB=2,AB∥DC,AD⊥CD,PC⊥平面ABCD.
如图,在四棱锥P一ABCD中,PC=AD=CD=$\frac{1}{2}$AB=2,AB∥DC,AD⊥CD,PC⊥平面ABCD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com