
| A. | [$\frac{1}{4}$,1] | B. | [0,$\frac{1}{4}$] | C. | [$\frac{1}{4}$,1) | D. | [1,+∞) |
分析 由题意可得存在y0∈[0,1],使f(y0)=y0成立,即f(x)=x在[0,1]上有解,即x-x2=a,x∈[0,1].利用二次函数的单调性求函数的值域,可得a的范围.
解答 解:由题意可得 y0=sinx0∈[-1,1],f(y0)=$\sqrt{{y}_{0}-a}$,
∵曲线y=sinx上存在点(x0,y0)使得f(f(y0))=y0,
∴存在y0∈[0,1],使f(y0)=y0成立,
即f(x)=x在[0,1]上有解,即 x-x2=a 在[0,1]上有解.
令g(x)=x-x2,则a为g(x)在[0,1]上的值域.
由g(x)=-$(x-\frac{1}{2})^{2}+\frac{1}{4}$,x∈[0,1],
∴g(x)∈$[0,\frac{1}{4}]$,即a∈$[0,\frac{1}{4}]$.
故选:B.
点评 本题考查了函数的单调性与值域,考查了推理能力与计算能力,属于中档题.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,+∞) | B. | (1,+∞) | C. | ($-\frac{1}{2}$,0)∪(2,+∞) | D. | (-1,0)∪(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{1}{2}$,+∞) | B. | [-$\frac{3}{2}$,+∞) | C. | [-1,+∞) | D. | [-2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
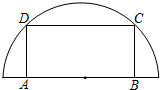 如图,在半径为30cm的半圆形铁皮上截取一块矩形材料A(点A,B在直径上,点C,D在半圆周上),并将其卷成一个以AD为母线的圆柱体罐子的侧面(不计剪裁和拼接损耗).
如图,在半径为30cm的半圆形铁皮上截取一块矩形材料A(点A,B在直径上,点C,D在半圆周上),并将其卷成一个以AD为母线的圆柱体罐子的侧面(不计剪裁和拼接损耗).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com