
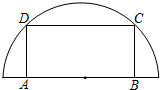
 如图,在半径为30cm的半圆形铁皮上截取一块矩形材料A(点A,B在直径上,点C,D在半圆周上),并将其卷成一个以AD为母线的圆柱体罐子的侧面(不计剪裁和拼接损耗).
如图,在半径为30cm的半圆形铁皮上截取一块矩形材料A(点A,B在直径上,点C,D在半圆周上),并将其卷成一个以AD为母线的圆柱体罐子的侧面(不计剪裁和拼接损耗).分析 (1)设BC=x,求出AB,得出侧面积S关于x的函数,利用基本不等式得出S的最大值;
(2)用x表示出圆柱的底面半径,得出体积V(x)关于x的函数,判断V(x)的单调性,得出V(x)的最大值.
解答 解:(1)连接OC,设BC=x,则AB=2$\sqrt{900-{x}^{2}}$,(其中0<x<30),
∴S=2x$\sqrt{900-{x}^{2}}$=2 $\sqrt{{x}^{2}(900-{x}^{2})}$≤x2+(900-x2)=900,
当且仅当x2=900-x2,即x=15$\sqrt{2}$时,S取最大值900;
∴取BC=15$\sqrt{2}$cm时,矩形ABCD的面积最大,最大值为900cm2.
(2)设圆柱底面半径为r,高为x,
则AB=2$\sqrt{900-{x}^{2}}$=2πr,解得r=$\frac{\sqrt{900-{x}^{2}}}{π}$,
∴V=πr2h=$\frac{1}{π}$(900x-x3),(其中0<x<30);
∴V′=$\frac{1}{π}$(900-3x2),令V′(x)=0,得x=10$\sqrt{3}$;
因此V(x)=$\frac{1}{π}$(900x-x3)在(0,10 $\sqrt{3}$)上是增函数,在(10$\sqrt{3}$,30)上是减函数;
∴当x=10$\sqrt{3}$时,V(x)取得最大值V(10$\sqrt{3}$)=$\frac{6000\sqrt{3}}{π}$,
∴取BC=10$\sqrt{3}$cm时,做出的圆柱形罐子体积最大,最大值为$\frac{6000\sqrt{3}}{π}$cm3.
点评 本题考查了圆柱的结构特征,圆柱的侧面积与体积计算,用不等式与函数单调性求函数最值,属于中档题.


 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:高中数学 来源: 题型:选择题
| A. | [$\frac{1}{4}$,1] | B. | [0,$\frac{1}{4}$] | C. | [$\frac{1}{4}$,1) | D. | [1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x2=2x1+1 | B. | x2=2x1 | C. | y2=2y1+1 | D. | y2=2y1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\sqrt{15}$ | C. | $\sqrt{34}$ | D. | $\frac{{\sqrt{34}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | $\frac{33}{5}$ | C. | 7 | D. | 15 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2]∪[2,+∞) | B. | [-4,-2]∪[0,+∞) | C. | (-∞,-4]∪[-2,+∞) | D. | (-∞,-4]∪[0,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [2,4] | B. | [2,+∞) | C. | [3,4] | D. | [2,3] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com