
| A. | [2,4] | B. | [2,+∞) | C. | [3,4] | D. | [2,3] |
分析 由题意可得-1≤-ax+x3+1≤1对x∈(0,$\sqrt{2}$]恒成立,即 x∈(0,$\sqrt{2}$]时,a≤x2+$\frac{2}{x}$ 和 a≥x2同时恒成立.利用导数求得x2+$\frac{2}{x}$ 的最小值,再求得x2的最大值,可得a的范围.
解答 解:由题意可得定义在R上的偶函数f(x)在[0,+∞)上递减,f(x)在(-∞,0]上递增,
且偶函数f(x)的图象关于y轴对称.
∵不等式f(-ax+x3+1)+f(ax-x3-1)≥2f(1)对x∈(0,$\sqrt{2}$]恒成立,f(-ax+x3+1)=f(ax-x3-1),
∴f(-ax+x3+1)≥f(1)对x∈(0,$\sqrt{2}$]恒成立,
∴-1≤-ax+x3+1≤1对x∈(0,$\sqrt{2}$]恒成立,
即 x∈(0,$\sqrt{2}$]时,a≤x2+$\frac{2}{x}$ 和 a≥x2同时恒成立.
令h(x)=x2+$\frac{2}{x}$,∵由 h′(x)=2x-$\frac{2}{{x}^{2}}$=$\frac{2{(x}^{3}-1)}{{x}^{2}}$=0,求得x=1,
在(0,1)上,h′(x)<0,在(1,$\sqrt{2}$]上,h′(x)>0,故h(x)的最小值为h(1)=3,∴a≤3 ①.
再根据 x∈(0,$\sqrt{2}$]时,a≥x2 恒成立,∴a≥2 ②.
结合①②可得,2≤a≤3.
故选:D
点评 本题主要考查函数的单调性和奇偶性的综合应用,导数与函数的单调性间的关系,函数的恒成立问题,属于中档题.


科目:高中数学 来源: 题型:解答题
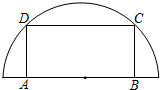 如图,在半径为30cm的半圆形铁皮上截取一块矩形材料A(点A,B在直径上,点C,D在半圆周上),并将其卷成一个以AD为母线的圆柱体罐子的侧面(不计剪裁和拼接损耗).
如图,在半径为30cm的半圆形铁皮上截取一块矩形材料A(点A,B在直径上,点C,D在半圆周上),并将其卷成一个以AD为母线的圆柱体罐子的侧面(不计剪裁和拼接损耗).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2)(3) | B. | (1)(4) | C. | (1)(2)(4) | D. | (1)(3)(4) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
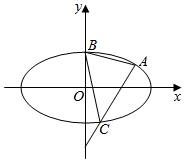 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1(a>b>0)$的焦距为2$\sqrt{3}$,一条准线方程为x=$\frac{4\sqrt{3}}{3}$.过点(0,-2)的直线l交椭圆于A,C两点(异于椭圆顶点),椭圆的上顶点为B,直线AB,BC的斜率分别为k1,k2.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1(a>b>0)$的焦距为2$\sqrt{3}$,一条准线方程为x=$\frac{4\sqrt{3}}{3}$.过点(0,-2)的直线l交椭圆于A,C两点(异于椭圆顶点),椭圆的上顶点为B,直线AB,BC的斜率分别为k1,k2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com