
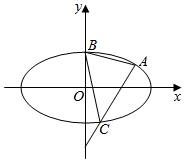
 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1(a>b>0)$的焦距为2$\sqrt{3}$,一条准线方程为x=$\frac{4\sqrt{3}}{3}$.过点(0,-2)的直线l交椭圆于A,C两点(异于椭圆顶点),椭圆的上顶点为B,直线AB,BC的斜率分别为k1,k2.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1(a>b>0)$的焦距为2$\sqrt{3}$,一条准线方程为x=$\frac{4\sqrt{3}}{3}$.过点(0,-2)的直线l交椭圆于A,C两点(异于椭圆顶点),椭圆的上顶点为B,直线AB,BC的斜率分别为k1,k2.分析 (1)由题意可得2c=2$\sqrt{3}$,$\frac{{a}^{2}}{c}$=$\frac{4\sqrt{3}}{3}$,a2=b2+c2,联立解出即可得出.
(2)设A(x0,y0),由∠CAB=90°,可得kAC•kAB=-1,化为:${y}_{0}^{2}+{y}_{0}$-2=-${x}_{0}^{2}$,由点A在椭圆上,可得$\frac{{x}_{0}^{2}}{4}$+${y}_{0}^{2}$=1,解得y0,x0.可得A,及其斜率kl.
(3)设A(x1,y1),B(x2,y2),直线l的方程为:y=kx-2,与椭圆方程联立化为:(1+4k2)x2-16kx+12=0,B(0,1),把根与系数的关系代入k1•k2=$\frac{{y}_{1}-1}{{x}_{1}}$$•\frac{{y}_{2}-1}{{x}_{2}}$=$\frac{{k}^{2}{x}_{1}{x}_{2}-3k({x}_{1}+{x}_{2})+9}{{x}_{1}{x}_{2}}$,即可得出.
解答 解:(1)∵2c=2$\sqrt{3}$,$\frac{{a}^{2}}{c}$=$\frac{4\sqrt{3}}{3}$,a2=b2+c2,
联立解得:c=$\sqrt{3}$,a=2,b=1,
∴椭圆C的标准方程为$\frac{{x}^{2}}{4}+{y}^{2}$=1.
(2)设A(x0,y0),∵∠CAB=90°,∴kAC•kAB=-1,
∴$\frac{{y}_{0}+2}{{x}_{0}}$•$\frac{{y}_{0}-1}{{x}_{0}}$=-1,化为:${y}_{0}^{2}+{y}_{0}$-2=-${x}_{0}^{2}$,
由点A在椭圆上,∴$\frac{{x}_{0}^{2}}{4}$+${y}_{0}^{2}$=1,∴${x}_{0}^{2}$=4-4${y}_{0}^{2}$,
∴$3{y}_{0}^{2}-{y}_{0}-2$=0,解得y0=1或-$\frac{2}{3}$,
∵A与B不重合,∴y0=-$\frac{2}{3}$,解得x0=$±\frac{2\sqrt{5}}{3}$.
∴A$(±\frac{2\sqrt{5}}{3},-\frac{2}{3})$.
∴kl=$±\frac{2\sqrt{5}}{5}$.
(3)设A(x1,y1),B(x2,y2),直线l的方程为:y=kx-2,
联立$\left\{\begin{array}{l}{y=kx-2}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$,化为:(1+4k2)x2-16kx+12=0,
∴x1+x2=$\frac{16k}{1+4{k}^{2}}$,x1x2=$\frac{12}{1+4{k}^{2}}$,B(0,1),
∴k1•k2=$\frac{{y}_{1}-1}{{x}_{1}}$$•\frac{{y}_{2}-1}{{x}_{2}}$=$\frac{(k{x}_{1}-3)(k{x}_{2}-3)}{{x}_{1}{x}_{2}}$=$\frac{{k}^{2}{x}_{1}{x}_{2}-3k({x}_{1}+{x}_{2})+9}{{x}_{1}{x}_{2}}$=$\frac{\frac{12{k}^{2}}{1+4{k}^{2}}-\frac{48{k}^{2}}{1+4{k}^{2}}+9}{\frac{12}{1+4{k}^{2}}}$=$\frac{3}{4}$.
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题、一元二次方程的根与系数的关系、斜率计算公式、相互垂直的直线斜率之间的关系,考查了推理能力与计算能力,属于难题.


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:高中数学 来源: 题型:选择题
| A. | [2,4] | B. | [2,+∞) | C. | [3,4] | D. | [2,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
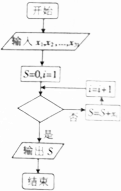 用xi表示某人2016年3月份第i天的手机流量,计算该人3月的手机流量总量的程序框图如图,则判断框中可以填入( )
用xi表示某人2016年3月份第i天的手机流量,计算该人3月的手机流量总量的程序框图如图,则判断框中可以填入( )| A. | i≤31? | B. | i<31? | C. | i>31? | D. | i≥31? |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{12}{7}$ | B. | $\frac{7}{3}$ | C. | $\frac{3}{7}$$\sqrt{21}$ | D. | $\frac{\sqrt{21}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | π | B. | 2π | C. | 4π | D. | 6π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com