
分析 (Ⅰ)由诱导公式与辅助角公式化简解析式,由此得到$f(\frac{π}{3})$的值和f(x)的最小正周期;
(Ⅱ)由x的范围得到2x+$\frac{π}{6}$的范围,由此得到f(x)的范围.
解答 解:(Ⅰ)∵f(x)=$\sqrt{3}cos(\frac{π}{2}-x)+2{cos^2}\frac{x}{2}$=$\sqrt{3}$sinx+cosx+1
=2sin(x+$\frac{π}{6}$)+1,
∴$f(\frac{π}{3})$=2,
f(x)的最小正周期是T=π.
(Ⅱ)当x∈[0,π]时,
2x+$\frac{π}{6}$∈[$\frac{π}{6}$,2π+$\frac{π}{6}$],
∴2sin(2x+$\frac{π}{6}$)∈[-2,2],
∴f(x)∈[-1,3].
点评 本题考查三角函数式的化简,以及由x的范围确定值域.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
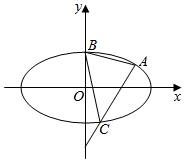 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1(a>b>0)$的焦距为2$\sqrt{3}$,一条准线方程为x=$\frac{4\sqrt{3}}{3}$.过点(0,-2)的直线l交椭圆于A,C两点(异于椭圆顶点),椭圆的上顶点为B,直线AB,BC的斜率分别为k1,k2.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1(a>b>0)$的焦距为2$\sqrt{3}$,一条准线方程为x=$\frac{4\sqrt{3}}{3}$.过点(0,-2)的直线l交椭圆于A,C两点(异于椭圆顶点),椭圆的上顶点为B,直线AB,BC的斜率分别为k1,k2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | $\frac{1}{2}$ | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x>0} | B. | {x|-1<x<1} | C. | {x|x>1} | D. | {x|x>0或x<-1} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com