
分析 列举出所有可能的基本事件和符合条件的基本事件,使用古典概型的概率计算公式计算概率.
解答 解:设剩余三名应聘者为a,b,c,则从5人中录用两人的所有可能结果共有10个,
分别为(甲,乙),(甲,a),(甲,b),(甲,c),(乙,a),(乙,b),(乙,c),(a,b),(a,c),(b,c).
其中甲乙两人至少有1人被录用的基本事件有7个,分别是(甲,乙),(甲,a),(甲,b),(甲,c),(乙,a),(乙,b),(乙,c).
∴甲、乙两人中至少有1人被录用的概率P=$\frac{7}{10}$.
故答案为:$\frac{7}{10}$
点评 本题考查了古典概型的概率计算,属于基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2]∪[2,+∞) | B. | [-4,-2]∪[0,+∞) | C. | (-∞,-4]∪[-2,+∞) | D. | (-∞,-4]∪[0,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [2,4] | B. | [2,+∞) | C. | [3,4] | D. | [2,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数f(x)是偶函数 | B. | 函数f(x)在[0,$\frac{π}{2}$]上单调递增 | ||
| C. | 函数f(x)是周期为π的周期函数 | D. | 函数f(x)的值域为[-1,$\frac{\sqrt{2}}{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
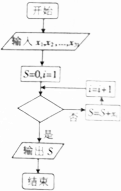 用xi表示某人2016年3月份第i天的手机流量,计算该人3月的手机流量总量的程序框图如图,则判断框中可以填入( )
用xi表示某人2016年3月份第i天的手机流量,计算该人3月的手机流量总量的程序框图如图,则判断框中可以填入( )| A. | i≤31? | B. | i<31? | C. | i>31? | D. | i≥31? |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{12}{7}$ | B. | $\frac{7}{3}$ | C. | $\frac{3}{7}$$\sqrt{21}$ | D. | $\frac{\sqrt{21}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com