
| A. | 5 | B. | $\frac{33}{5}$ | C. | 7 | D. | 15 |
分析 作出不等式组对应的平面区域,根据直线平行求出目标函数的最大值和最小值建立方程关系进行求解即可.
解答 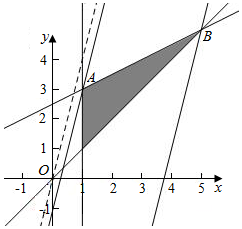 解:作出不等式组对应的平面区域如图,
解:作出不等式组对应的平面区域如图,
由z=4x-y得y=4x-z,
平移直线y=4x-z,由图象知,当直线y=4x-z经过A时,直线的截距最大,此时z最小,
经过点B时,直线的截距最小,此时z最大,
由$\left\{\begin{array}{l}{x=1}\\{x-2y+m=0}\end{array}\right.$得$\left\{\begin{array}{l}{x=1}\\{y=\frac{1+m}{2}}\end{array}\right.$,即A(1,$\frac{1+m}{2}$),此时z最小值为z=4-$\frac{1+m}{2}$,
由$\left\{\begin{array}{l}{x-2y+5=0}\\{x-y=0}\end{array}\right.$得$\left\{\begin{array}{l}{x=5}\\{y=5}\end{array}\right.$,即B(5,5),此时z最大值为z=4×5-5=15,
∵z=4x-y的最大值是最小值的15倍,
∴15=15(4-$\frac{1+m}{2}$),即4-$\frac{1+m}{2}$=1,
得$\frac{1+m}{2}$=3,
即m=5,
故选:A
点评 本题主要考查线性规划的应用,利用数形结合求出目标函数的最优解,建立方程关系是解决本题的关键.


科目:高中数学 来源: 题型:选择题
| A. | (2,+∞) | B. | (1,+∞) | C. | ($-\frac{1}{2}$,0)∪(2,+∞) | D. | (-1,0)∪(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
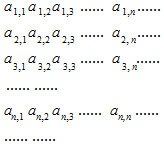 如图所示的正数数阵中,第一横行是公差为d的等差数列,奇数列均是公比为q1等比数列,偶数列均是公比为q2等比数列,已知a1,1=1,a1,4=7,a4,1=$\frac{1}{8}$,a2,4=2(a1,1+a2,2)则下列结论中不正确的是( )
如图所示的正数数阵中,第一横行是公差为d的等差数列,奇数列均是公比为q1等比数列,偶数列均是公比为q2等比数列,已知a1,1=1,a1,4=7,a4,1=$\frac{1}{8}$,a2,4=2(a1,1+a2,2)则下列结论中不正确的是( )| A. | d+q1+q2=a2,5 | |
| B. | a2,1+a2,3+a2,5+…+a2,21=$\frac{441}{2}$ | |
| C. | a1,2+a3,2+a5,2+…+a21,2=411-1 | |
| D. | ai,j=$\left\{\begin{array}{l}(2j-1){2^{1-i}},j为正奇数\\(2j-1){2^{i-1}},j为正偶数\end{array}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
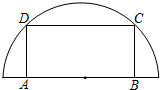 如图,在半径为30cm的半圆形铁皮上截取一块矩形材料A(点A,B在直径上,点C,D在半圆周上),并将其卷成一个以AD为母线的圆柱体罐子的侧面(不计剪裁和拼接损耗).
如图,在半径为30cm的半圆形铁皮上截取一块矩形材料A(点A,B在直径上,点C,D在半圆周上),并将其卷成一个以AD为母线的圆柱体罐子的侧面(不计剪裁和拼接损耗).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 为了研究某校的高三市三模的文科数学成绩,现随机抽取了60名学生的数学成绩进行分析,现将成绩按如下方式分为6组,第一组[80,90),第二组[90,100),…,第六组[130,140),得到如图所示的频率分布直方图.
为了研究某校的高三市三模的文科数学成绩,现随机抽取了60名学生的数学成绩进行分析,现将成绩按如下方式分为6组,第一组[80,90),第二组[90,100),…,第六组[130,140),得到如图所示的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com