
分析 根据奇函数的性质可得f(0)=0,由条件可得f(3)=f(-3)+f(3)=0,f(x)+3=f(x+6),函数值呈等差数列关系,进而求出结果.
解答 解:奇函数f(x),∴f(0)=0,
f(x)对任意x∈R都有f(x+6)=f(x)+3成立,f(6)=f(0)+3,
f(12)=f(6)+3=f(0)+3×2,
f(18)=f(12)+3=f(0)+3×3,
…
f(2016)=f(336×6+0)=336×3=1008
f(2015)=f(336×6-1)=336×3+f(-1)=1008-1=1007
∴f(2015)+f(2016)=2015.
故答案为:2015.
点评 考查了奇函数的性质和函数形状的应用,属于常规题型,应熟练掌握.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{1}{2}$,+∞) | B. | [-$\frac{3}{2}$,+∞) | C. | [-1,+∞) | D. | [-2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
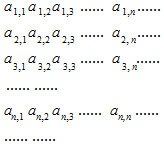 如图所示的正数数阵中,第一横行是公差为d的等差数列,奇数列均是公比为q1等比数列,偶数列均是公比为q2等比数列,已知a1,1=1,a1,4=7,a4,1=$\frac{1}{8}$,a2,4=2(a1,1+a2,2)则下列结论中不正确的是( )
如图所示的正数数阵中,第一横行是公差为d的等差数列,奇数列均是公比为q1等比数列,偶数列均是公比为q2等比数列,已知a1,1=1,a1,4=7,a4,1=$\frac{1}{8}$,a2,4=2(a1,1+a2,2)则下列结论中不正确的是( )| A. | d+q1+q2=a2,5 | |
| B. | a2,1+a2,3+a2,5+…+a2,21=$\frac{441}{2}$ | |
| C. | a1,2+a3,2+a5,2+…+a21,2=411-1 | |
| D. | ai,j=$\left\{\begin{array}{l}(2j-1){2^{1-i}},j为正奇数\\(2j-1){2^{i-1}},j为正偶数\end{array}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,4] | B. | (1,2)∪(4,+∞) | C. | (4,+∞) | D. | (1,4) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
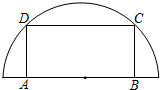 如图,在半径为30cm的半圆形铁皮上截取一块矩形材料A(点A,B在直径上,点C,D在半圆周上),并将其卷成一个以AD为母线的圆柱体罐子的侧面(不计剪裁和拼接损耗).
如图,在半径为30cm的半圆形铁皮上截取一块矩形材料A(点A,B在直径上,点C,D在半圆周上),并将其卷成一个以AD为母线的圆柱体罐子的侧面(不计剪裁和拼接损耗).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com