
ЁОЬтФПЁПЮЊСЫЗжЮіФГИіИпШ§бЇЩњЕФбЇЯАзДЬЌ,ЖдЦфЯТвЛИіНзЖЮЕФбЇЯАЬсГіжИЕМадНЈвщ,ФГРЯЪІЯжЖдЫћЧА7ДЮПМЪдЕФЪ§бЇГЩМЈxЁЂЮяРэГЩМЈyНјааЗжЮі.ЯТУцЪЧИУбЇЩњ7ДЮПМЪдЕФГЩМЈ.

(1)ЫћЕФЪ§бЇГЩМЈгыЮяРэГЩМЈФФИіИќЮШЖЈ?ЧыИјГіФуЕФжЄУї.
(2)вбжЊИУбЇЩњЕФЮяРэГЩМЈyгыЪ§бЇГЩМЈxЪЧЯпадЯрЙиЕФ,ШєИУбЇЩњЕФЮяРэГЩМЈДяЕН115Зж,ЧыФуЙРМЦЫћЕФЪ§бЇГЩМЈДѓдМЪЧЖрЩй?ВЂЧыФуИљОнЮяРэГЩМЈгыЪ§бЇГЩМЈЕФЯрЙиад,ИјГіИУбЇЩњдкбЇЯАЪ§бЇЁЂЮяРэЩЯЕФКЯРэНЈвщ.
ЁОД№АИЁПЃЈ1ЃЉМћНтЮіЃЛЃЈ2ЃЉМћНтЮі
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнБэжаЕФЪ§ОнЃЌЧѓЕУ![]() ЃЌНјЖјЧѓЕУЪ§бЇКЭЮяРэЕФЗНВюЃЌБШНЯДѓаЁЃЌМДПЩПЩЕУНсТлЃЛ
ЃЌНјЖјЧѓЕУЪ§бЇКЭЮяРэЕФЗНВюЃЌБШНЯДѓаЁЃЌМДПЩПЩЕУНсТлЃЛ
ЃЈ2ЃЉгЩгк![]() гы
гы![]() жЎМфОпгаЯпадЯрЙиЙиЯЕ,РћгУЙЋЪНЧѓЕУ
жЎМфОпгаЯпадЯрЙиЙиЯЕ,РћгУЙЋЪНЧѓЕУ![]() ЕФжЕЃЌЧѓЕУЛиЙщжБЯпЕФЗНГЬЃЌСю
ЕФжЕЃЌЧѓЕУЛиЙщжБЯпЕФЗНГЬЃЌСю![]() ЃЌЧѓЕУ
ЃЌЧѓЕУ![]() ЕФжЕЃЌМДПЩЕУЕННсТл.
ЕФжЕЃЌМДПЩЕУЕННсТл.
(1)гЩБэжаЪ§ОнЕУ![]() =100+
=100+![]() =100;
=100;
![]() =100+
=100+![]() =100.
=100.
Ёр![]() =
=![]() =142,
=142,![]() =
=![]() .Ёп
.Ёп![]() >
>![]() ,ЁрЮяРэГЩМЈИќЮШЖЈ.
,ЁрЮяРэГЩМЈИќЮШЖЈ.
(2)гЩгкxгыyжЎМфОпгаЯпадЯрЙиЙиЯЕ,ЩшЯпадЛиЙщЗНГЬЮЊ![]() ,
,
ИљОнЛиЙщЯЕЪ§ЙЋЪНЕУЕН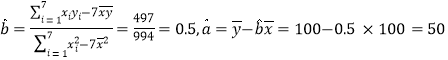 ЃЌ
ЃЌ
ЁрЯпадЛиЙщЗНГЬЮЊ![]() =0.5x+50.
=0.5x+50.
ЕБ![]() =115ЪБ,x=130,МДИУбЇЩњЕФЮяРэГЩМЈДяЕН115ЗжЪБ,ЫћЕФЪ§бЇГЩМЈДѓдМЮЊ130Зж.
=115ЪБ,x=130,МДИУбЇЩњЕФЮяРэГЩМЈДяЕН115ЗжЪБ,ЫћЕФЪ§бЇГЩМЈДѓдМЮЊ130Зж.
НЈвщ:НјвЛВНМгЧПЖдЪ§бЇЕФбЇЯА,ЬсИпЪ§бЇГЩМЈЕФЮШЖЈад,НЋгажњгкЮяРэГЩМЈЕФНјвЛВНЬсИп.


 КЎМйДѓДЎСЊЛЦЩНЪщЩчЯЕСаД№АИ
КЎМйДѓДЎСЊЛЦЩНЪщЩчЯЕСаД№АИ КЎМйДДаТаЭзджїбЇЯАЕкШ§бЇЦкКЎМйЯЮНгЯЕСаД№АИ
КЎМйДДаТаЭзджїбЇЯАЕкШ§бЇЦкКЎМйЯЮНгЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПИјГіЯТСаЮхИіУќЬтЃК
ЂйНЋAЃЌBЃЌCШ§жжИіЬхАД3ЁУ1ЁУ2ЕФБШР§ЗжВуГщбљЕїВщЃЌШєГщШЁЕФAжжИіЬхга9ИіЃЌдђбљБОШнСПЮЊ30ЃЛ
ЂквЛзщЪ§Он1ЃЌ2ЃЌ3ЃЌ3ЃЌ4ЃЌ5ЕФЦНОљЪ§ЁЂжкЪ§ЁЂжаЮЛЪ§ЖМЯрЭЌЃЛ
ЂлМззщЪ§ОнЕФЗНВюЮЊ5ЃЌввзщЪ§ОнЮЊ5ЃЌ6ЃЌ9ЃЌ10ЃЌ5ЃЌФЧУДетСНзщЪ§ОнжаБШНЯЮШЖЈЕФЪЧМзЃЛ
ЂмвбжЊОпгаЯрЙиЙиЯЕЕФСНИіБфСПТњзуЕФЛиЙщжБЯпЗНГЬЮЊ![]() ЃН1Ѓ2xЃЌдђxУПдіМг1ИіЕЅЮЛЃЌyЦНОљМѕЩй2ИіЕЅЮЛЃЛ
ЃН1Ѓ2xЃЌдђxУПдіМг1ИіЕЅЮЛЃЌyЦНОљМѕЩй2ИіЕЅЮЛЃЛ
ЂнЭГМЦЕФ10ИібљБОЪ§ОнЮЊ125ЃЌ120ЃЌ122ЃЌ105ЃЌ130ЃЌ114ЃЌ116ЃЌ95ЃЌ120ЃЌ134ЃЌдђбљБОЪ§ОнТфдк[114.5ЃЌ124.5)ФкЕФЦЕТЪЮЊ0.4.
ЦфжаЪЧецУќЬтЕФЮЊ(ЁЁЁЁ)
A. ЂйЂкЂм B. ЂкЂмЂн C. ЂкЂлЂм D. ЂлЂмЂн
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊХзЮяЯпy2=4xЕФНЙЕуЮЊF,A,BЮЊХзЮяЯпЩЯСНЕу,Шє![]() OЮЊзјБъдЕу,дђЁїAOBЕФУцЛ§ЮЊ( )
OЮЊзјБъдЕу,дђЁїAOBЕФУцЛ§ЮЊ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЭждВC1:![]() (a>b>0)ЕФРыаФТЪЮЊ
(a>b>0)ЕФРыаФТЪЮЊ![]() ,xжсБЛЧњЯпC2:y=x2-bНиЕУЕФЯпЖЮГЄЖШЕШгкC1ЕФЖЬжсГЄ.вбжЊC2гыyжсЕФНЛЕуЮЊM,Й§зјБъдЕуOЕФжБЯпlгыC2ЯрНЛгкЕуA,B,жБЯпMA,MBЗжБ№гыC1ЯрНЛгкЕуD,E.
,xжсБЛЧњЯпC2:y=x2-bНиЕУЕФЯпЖЮГЄЖШЕШгкC1ЕФЖЬжсГЄ.вбжЊC2гыyжсЕФНЛЕуЮЊM,Й§зјБъдЕуOЕФжБЯпlгыC2ЯрНЛгкЕуA,B,жБЯпMA,MBЗжБ№гыC1ЯрНЛгкЕуD,E.
(1)ЧѓC1,C2ЕФЗНГЬ;
(2)ЧѓжЄ:MAЁЭMB;
(3)МЧЁїMAB,ЁїMDEЕФУцЛ§ЗжБ№ЮЊS1,S2,Шє![]() ,ЧѓІЫЕФШЁжЕЗЖЮЇ.
,ЧѓІЫЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП8ШЫЮЇдВзРПЊЛсЃЌЦфжае§ЁЂИБзщГЄИї1ШЫЃЌМЧТМдБ1ШЫ.
(1)Шєе§ЁЂИБзщГЄЯрСкЖјзјЃЌгаЖрЩйжжзјЗЈЃП
(2)ШєМЧТМдБзјгке§ЁЂИБзщГЄжЎМфЃЌгаЖрЩйжжзјЗЈЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШєКЏЪ§![]() ЮЊЖЈвхгђ
ЮЊЖЈвхгђ![]() ЩЯЕЅЕїКЏЪ§ЃЌЧвДцдкЧјМф
ЩЯЕЅЕїКЏЪ§ЃЌЧвДцдкЧјМф![]() ЃЈЦфжа
ЃЈЦфжа![]() ЃЉЃЌЪЙЕУЕБ
ЃЉЃЌЪЙЕУЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЕФШЁжЕЗЖЮЇЧЁЮЊ
ЕФШЁжЕЗЖЮЇЧЁЮЊ![]() ЃЌдђГЦКЏЪ§
ЃЌдђГЦКЏЪ§![]() ЪЧ
ЪЧ![]() ЩЯЕФе§КЏЪ§ЃЌЧјМф
ЩЯЕФе§КЏЪ§ЃЌЧјМф![]() НазіЕШгђЧјМфЃЎ
НазіЕШгђЧјМфЃЎ
ЃЈ1ЃЉвбжЊ![]() ЪЧ
ЪЧ![]() ЩЯЕФе§КЏЪ§ЃЌЧѓ
ЩЯЕФе§КЏЪ§ЃЌЧѓ![]() ЕФЕШгђЧјМфЃЛ
ЕФЕШгђЧјМфЃЛ
ЃЈ2ЃЉЪдЬНОПЪЧЗёДцдкЪЕЪ§![]() ЃЌЪЙЕУКЏЪ§
ЃЌЪЙЕУКЏЪ§![]() ЪЧ
ЪЧ![]() ЩЯЕФе§КЏЪ§ЃПШєДцдкЃЌЧыЧѓГіЪЕЪ§
ЩЯЕФе§КЏЪ§ЃПШєДцдкЃЌЧыЧѓГіЪЕЪ§![]() ЕФШЁжЕЗЖЮЇЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЕФШЁжЕЗЖЮЇЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩшКЏЪ§fЃЈxЃЉ=xexЉasinxcosxЃЈaЁЪRЃЌЦфжаeЪЧздШЛЖдЪ§ЕФЕзЪ§ЃЉЃЎ
ЃЈ1ЃЉЕБa=0ЪБЃЌЧѓfЃЈxЃЉЕФМЋжЕЃЛ
ЃЈ2ЃЉШєЖдгкШЮвтЕФxЁЪ[0ЃЌ ![]() ]ЃЌfЃЈxЃЉЁн0КуГЩСЂЃЌЧѓaЕФШЁжЕЗЖЮЇЃЛ
]ЃЌfЃЈxЃЉЁн0КуГЩСЂЃЌЧѓaЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉЪЧЗёДцдкЪЕЪ§aЃЌЪЙЕУКЏЪ§fЃЈxЃЉдкЧјМф ![]() ЩЯгаСНИіСуЕуЃПШєДцдкЃЌЧѓГіaЕФШЁжЕЗЖЮЇЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЩЯгаСНИіСуЕуЃПШєДцдкЃЌЧѓГіaЕФШЁжЕЗЖЮЇЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЫФРтзЖ![]() жаЃЌЕзУц
жаЃЌЕзУц![]() ЪЧЦНааЫФБпаЮЃЌ
ЪЧЦНааЫФБпаЮЃЌ ![]() ЦНУц
ЦНУц![]() ЃЌЕу
ЃЌЕу![]() ЃЌ
ЃЌ ![]() ЗжБ№ЮЊ
ЗжБ№ЮЊ![]() ЃЌ
ЃЌ ![]() ЕФжаЕуЃЌЧв
ЕФжаЕуЃЌЧв![]() ЃЌ
ЃЌ ![]() .
.

ЃЈ1ЃЉжЄУїЃК ![]() ЦНУц
ЦНУц![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЩшжБЯп![]() гыЦНУц
гыЦНУц![]() ЫљГЩНЧЮЊ
ЫљГЩНЧЮЊ![]() ЃЌЕБ
ЃЌЕБ![]() дк
дк![]() ФкБфЛЏЪБЃЌЧѓЖўУцНЧ
ФкБфЛЏЪБЃЌЧѓЖўУцНЧ![]() ЕФШЁжЕЗЖЮЇ.
ЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкжБНЧзјБъЯЕжаЃЌвбжЊдВ![]() ЕФдВаФзјБъЮЊ
ЕФдВаФзјБъЮЊ![]() ЃЌАыОЖЮЊ
ЃЌАыОЖЮЊ![]() ЃЌвдзјБъдЕуЮЊМЋЕуЃЌ
ЃЌвдзјБъдЕуЮЊМЋЕуЃЌ![]() жсЕФе§АыжсЮЊМЋжсНЈСЂМЋзјБъЯЕЃЌжБЯпlЕФВЮЪ§ЗНГЬЮЊЃК
жсЕФе§АыжсЮЊМЋжсНЈСЂМЋзјБъЯЕЃЌжБЯпlЕФВЮЪ§ЗНГЬЮЊЃК![]() ЃЈ
ЃЈ![]() ЮЊВЮЪ§ЃЉЃЎ
ЮЊВЮЪ§ЃЉЃЎ
ЃЈ1ЃЉЧѓдВ![]() КЭжБЯпlЕФМЋзјБъЗНГЬЃЛ
КЭжБЯпlЕФМЋзјБъЗНГЬЃЛ
ЃЈ2ЃЉЕу![]() ЕФМЋзјБъЮЊ
ЕФМЋзјБъЮЊ![]() ЃЌжБЯпlгыдВ
ЃЌжБЯпlгыдВ![]() ЯрНЛгкAЃЌBЃЌЧѓ
ЯрНЛгкAЃЌBЃЌЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com