
(本小题满分12分)如图,正三棱柱ABC—A1B1C1中,D是BC的中点,AA1=AB=1.
(I)求证:A1C//平面AB1D;
(II)求二面角B—AB1—D的大小;
(III)求点C到平面AB1D的距离.
(I)空间直角坐标系D—xyz,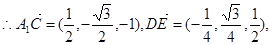
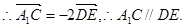
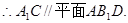 (II)
(II)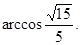 (III)
(III)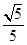
解析试题分析:建立空间直角坐标系D—xyz,如图,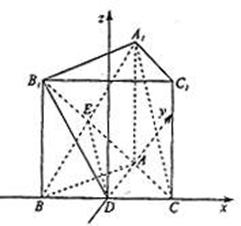
(1)证明:
连接A1B,设A1B∩AB1 = E,连接DE.
设A1A =" AB" = 1,
则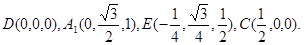
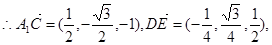
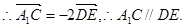 …………………………3分
…………………………3分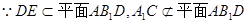 ,
,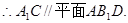 ……………………………………4分
……………………………………4分
(2)解: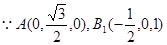 ,
, 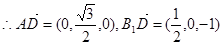 ,
,
设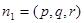 是平面AB1D的法向量,则
是平面AB1D的法向量,则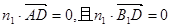 ,
,
故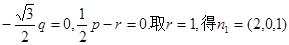 ;
;
同理,可求得平面AB1B的法向量是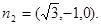 ……………………6分
……………………6分
设二面角B—AB1—D的大小为θ,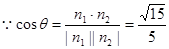 ,
,
∴二面角B—AB1—D的大小为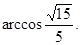 …………………………8分
…………………………8分
(3)解由(II)得平面AB1D的法向量为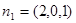 ,
,
取其单位法向量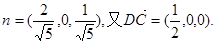
∴点C到平面AB1D的距离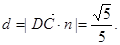
考点:线面平行的判定及二面角,点面距
点评:本题第二问还可作出平面角求解,第三问利用等体积法亦可求解


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:高中数学 来源: 题型:解答题
如图,在三棱锥 中,
中, 底面
底面 ,点
,点 ,
, 分别在棱
分别在棱 上,且
上,且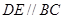

(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)当 为
为 的中点时,求
的中点时,求 与平面
与平面 所成的角的正弦值;
所成的角的正弦值;
(Ⅲ)是否存在点 使得二面角
使得二面角 为直二面角?若存在,请确定点E的位置;若不存在,请说明理由.
为直二面角?若存在,请确定点E的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分14分)
如图,四棱锥S-ABCD中,SA⊥平面ABCD,底面ABCD为直角梯形,AD∥BC,∠BAD=90 ,且BC=2AD=2,AB=4,SA=3.
(1)求证:平面SBC⊥平面SAB;
(2)若E、F分别为线段BC、SB上的一点(端点除外),满足 .(
.( )
)
①求证:对于任意的 ,恒有SC∥平面AEF;
,恒有SC∥平面AEF;
②是否存在 ,使得△AEF为直角三角形,若存在,求出所有符合条件的
,使得△AEF为直角三角形,若存在,求出所有符合条件的 值;若不存在,说明理由.
值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分为10分)
在四面体ABCD中作截面PQR,若PQ,CB的延长线交于M;RQ,DB的延长线交于N;RP,DC的延长线交于K,求证:M、N、K三点共线.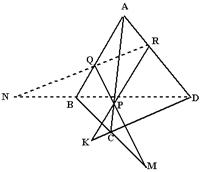
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分) 如图,平面 ⊥平面
⊥平面 ,其中
,其中 为矩形,
为矩形, 为梯形,
为梯形, ∥
∥ ,
, ⊥
⊥ ,
, =
= =2
=2 =2,
=2, 为
为 中点.
中点.
(Ⅰ) 证明 ;
;
(Ⅱ) 若二面角 的平面角的余弦值为
的平面角的余弦值为 ,求
,求 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分)如图所示,已知四棱锥S—ABCD的底面ABCD是矩形,M、N分别是CD、SC的中点,SA⊥底面ABCD,SA=AD=1,AB= .
.
(1)求证:MN⊥平面ABN;(2)求二面角A—BN—C的余弦值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com