
分析 (Ⅰ)求出a=1;设x∈[0,1],则-x∈[-1,0],利用条件,即可写出f(x)在[0,1]上的解析式;
(Ⅱ)利用换元法求f(x)在[0,1]上的最大值.
解答 解:(Ⅰ)∵f(x)为定义在[-1,1]上的奇函数,且f(x)在x=0处有意义,
∴f(0)=0,即f(0)=$\frac{1}{40}$-$\frac{a}{20}$=1-a=0.
∴a=1.…(3分)
设x∈[0,1],则-x∈[-1,0].
∴f(-x)=$\frac{1}{4-x}$-$\frac{1}{2-x}$=4x-2x.
又∵f(-x)=-f(x)
∴-f(x)=4x-2x.
∴f(x)=2x-4x.…(8分)
(Ⅱ)当x∈[0,1],f(x)=2x-4x=2x-(2x)2,
∴设t=2x(t>0),则f(t)=t-t2.
∵x∈[0,1],∴t∈[1,2].
当t=1时,取最大值,最大值为1-1=0.…(12分)
点评 本题考查函数的奇偶性,考查函数解析式的确定,考查函数的最值,考查学生的计算能力,属于中档题.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:高中数学 来源: 题型:解答题
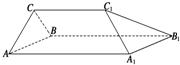 如图所示的几何体中,四边形AA1B1B是边长为3的正方形,CC1=2,CC1∥AA1,这个几何体是棱柱吗?若是,指出是几棱柱.若不是棱柱,请你试用一个平面截去一部分,使剩余部分是一个棱长为2的三棱柱,并指出截去的几何体的特征,在立体图中画出截面.
如图所示的几何体中,四边形AA1B1B是边长为3的正方形,CC1=2,CC1∥AA1,这个几何体是棱柱吗?若是,指出是几棱柱.若不是棱柱,请你试用一个平面截去一部分,使剩余部分是一个棱长为2的三棱柱,并指出截去的几何体的特征,在立体图中画出截面.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{AB}$+$\overrightarrow{CD}$+$\overrightarrow{BC}$ | B. | $\overrightarrow{AD}$+$\overrightarrow{EB}$+$\overrightarrow{BC}$+$\overrightarrow{CE}$ | C. | $\overrightarrow{MB}$-$\overrightarrow{MA}$+$\overrightarrow{BD}$ | D. | $\overrightarrow{CB}$+$\overrightarrow{AD}$-$\overrightarrow{BC}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
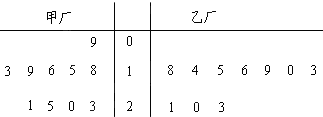
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-{log_2}3-\frac{1}{3}$ | B. | ${log_2}3-\frac{1}{3}$ | C. | $-{log_2}3+\frac{1}{3}$ | D. | ${log_2}3+\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | -1 | C. | i | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com