
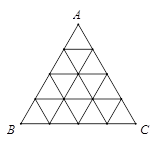
如图,将正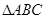 分割成16个全等的小正三角形,在每个三角形的顶点各放置一个数,使位于同一直线上的点放置的数(当数的个数不少于3时)都分别依次成等差数列,若顶点
分割成16个全等的小正三角形,在每个三角形的顶点各放置一个数,使位于同一直线上的点放置的数(当数的个数不少于3时)都分别依次成等差数列,若顶点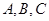 处的三个数互不相同且和为1,则所有顶点的数之和
处的三个数互不相同且和为1,则所有顶点的数之和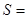 .
.
5
解析试题分析:根据等差中项法分别求解n=2,3,4时的值,由此归纳出f(n)的值即可.解:由题意可得,(各点放的数用该点的坐标表示)当n=2时,根据等差数列的性质可得,A+B=2D,A+C=2E,B+C=2F,且A+B+C=1,2(D+E+F)=2(A+B+C)=2,D+E+F=1,∴f(2)=2=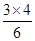 ,当n=3时,根据等差数列的性质可得,A+B=D+E,A+C=I+H,B+C=F+G,且A+B+C=1,从而可得D+E+H+I+F+F=2(A+B+C)=2,同样根据等差中项可得,M的数为
,当n=3时,根据等差数列的性质可得,A+B=D+E,A+C=I+H,B+C=F+G,且A+B+C=1,从而可得D+E+H+I+F+F=2(A+B+C)=2,同样根据等差中项可得,M的数为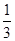 ,所以
,所以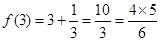 ,依次可知结论为
,依次可知结论为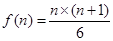 ,那么可知顶点
,那么可知顶点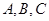 处的三个数互不相同且和为1,则n=5时,所有顶点的数之和
处的三个数互不相同且和为1,则n=5时,所有顶点的数之和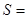 5,故答案为5.
5,故答案为5.
考点:数列的通项公式
点评:本题目主要考查了数列的通项公式的求解在实际问题中的应用,解题的关键是灵活利用等差中项,进行求解.考查了考试发现问题、解决问题的能力.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
.根据下面一组等式
S1=1
S2=2+3=5
S3=4+5+6=15
S4=7+8+9+10=34
S5=11+12+13+14+15=65
S6=16+17+18+19+20+21=111
S7=22+23+24+25+26+27+28=175
… … … … … … … …
可得 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
蜜蜂被认为是自然界中最杰出的建筑师,单个蜂巢可以近似地看作是一个正六边形,如图为一组蜂巢的截面图. 其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,以 表示第
表示第 幅图的蜂巢总数.则
幅图的蜂巢总数.则 =_____;
=_____; =___________.
=___________.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
定义:对于各项均为整数的数列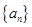 ,如果
,如果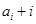 (
(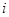 =1,2,3, )为完全平方数,则称数列
=1,2,3, )为完全平方数,则称数列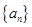 具有“
具有“ 性质”;不论数列
性质”;不论数列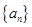 是否具有“
是否具有“ 性质”,如果存在数列
性质”,如果存在数列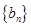 与
与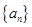 不是同一数列,且
不是同一数列,且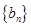 满足下面两个条件:
满足下面两个条件:
(1)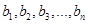 是
是 的一个排列;
的一个排列;
(2)数列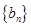 具有“
具有“ 性质”,则称数列
性质”,则称数列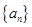 具有“变换
具有“变换 性质”.
性质”.
给出下面三个数列:
①数列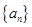 的前
的前 项和
项和 ;
;
②数列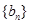 :1,2,3,4,5;
:1,2,3,4,5;
③数列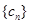 :1,2,3,4,5,6,7,8,9,10,11.
:1,2,3,4,5,6,7,8,9,10,11.
具有“ 性质”的为 ;具有“变换
性质”的为 ;具有“变换 性质”的为 .
性质”的为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com