
如图所示,已知圆O外有一点P,作圆O的切线PM,M为切点,过PM的中点N,作割线NAB,交圆于A、B两点,连接PA并延长,交圆O于点C,连接PB交圆O于点D,若MC=BC.
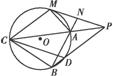
(1)求证:△APM∽△ABP;
(2)求证:四边形PMCD是平行四边形.
证明:(1)∵PM是圆O的切线,NAB是圆O的割线,N是PM的中点,
∴MN2=PN2=NA·NB, ∴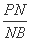 =
= ,
,
又∵∠PNA=∠BNP, ∴△PNA∽△BNP,
∴∠APN=∠PBN, 即∠APM=∠PBA.
∵MC=BC, ∴∠MAC=∠BAC,
∴∠MAP=∠PAB,
∴△APM∽△ABP.
(2)∵∠ACD=∠PBN,
∴∠ACD=∠PBN=∠APN,即∠PCD=∠CPM,
∴PM∥CD,
∵△APM∽△ABP,∴∠PMA=∠BPA,
∵PM是圆O的切线,∴∠PMA=∠MCP,
∴∠PMA=∠BPA=∠MCP,即∠MCP=∠DPC,
∴MC∥PD,
∴四边形PMCD是平行四边形.


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:高中数学 来源: 题型:
在抛物线y=x2+ax-5(a≠0)上取横坐标为x1=-4,x2=2的两点,过这两点引一条割线,有平行于该割线的一条直线同时与抛物线和圆5x2+5y2=36相切,则抛物线顶点的坐标为( )
(A)(-2,-9) (B)(0,-5)
(C)(2,-9) (D)(1,-6)
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,直线AB为圆的切线,切点为B,点C在圆上,∠ABC的角平分线BE交圆于点E,DB垂直BE交圆于点D.

(1)证明:DB=DC;
(2)设圆的半径为1,BC= ,延长CE交AB于点F,求△BCF外接圆的半径.
,延长CE交AB于点F,求△BCF外接圆的半径.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图所示,PC与圆O相切于点C,直线PO交圆O于A,B两点,弦CD垂直AB于E,则下面结论中,错误的结论是( )

(A)△BEC∽△DEA
(B)∠ACE=∠ACP
(C)DE2=OE·EP
(D)PC2=PA·AB
查看答案和解析>>
科目:高中数学 来源: 题型:
如图所示,已知两个正方形ABCD和DCEF不在同一平面内,M,N分别为AB,DF的
中点.

(1)若CD=2,平面ABCD⊥平面DCEF,求MN的长;
(2)用反证法证明:直线ME与BN是两条异面直线.
查看答案和解析>>
科目:高中数学 来源: 题型:
在△ABC中,角A,B,C的对边分别为a,b,c,且cos(A-B)cos B-sin(A-B)sin(A+C)
=-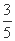 .
.
(1)求sin A的值;
(2)若a=4 ,b=5,求向量
,b=5,求向量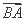 在
在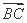 方向上的投影.
方向上的投影.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com