练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图,直线AB为圆的切线,切点为B,点C在圆上,∠ABC的角平分线BE交圆于点E,DB垂直BE交圆于点D.

    (1)证明:DB=DC;

    (2)设圆的半径为1,BC=,延长CE交AB于点F,求△BCF外接圆的半径.


     (1)证明:连接DE,交BC于点G.

    由弦切角定理得,

    ∠ABE=∠BCE.

    而∠ABE=∠CBE,

    故∠CBE=∠BCE,BE=CE.

    又DB⊥BE,

    所以DE为直径,

    则∠DCE=90°,

    由勾股定理可得DB=DC.

    (2)解:由(1)知,∠CDE=∠BDE,DB=DC,

    故DG是BC的中垂线,

    所以BG=.

    设DE的中点为O,连接BO,

    则∠BOG=60°.

    从而∠ABE=∠BCE=∠CBE=30°,

    所以CF⊥BF,

    故Rt△BCF外接圆的半径等于.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    若二次函数f(x)=ax2+bx+c(a≠0)的图象和直线y=x无交点,现有下列结论:①方程f(f(x))=x一定没有实数根;

    ②若a>0,则不等式f(f(x))>x对一切实数x都成立;

    ③若a<0,则必存在实数x0,使f(f(x0))>x0;

    ④若a+b+c=0,则不等式f(f(x))<x对一切实数都成立;

    ⑤函数g(x)=ax2-bx+c的图象与直线y=-x也一定没有交点.

    其中正确的结论是　　　　(写出所有正确结论的编号). 

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)=4x+ (x>0,a>0)在x=3时取得最小值,则a=　　　　. 

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设M是△ABC内一点,且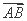·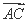=2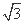,∠BAC=30°,定义f(M)=(m,n,p),其中m、n、p分别是△MBC、△MCA、△MAB的面积,若f(M)=(,x,y),则+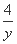的最小值是　　　　. 

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图,☉O和☉O′相交于A,B两点,过A作两圆的切线分别交两圆于C、D两点,连结DB并延长交☉O于点E.证明:

    (1)AC·BD=AD·AB;

    (2)AC=AE.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图所示,已知C点在圆O直径BE的延长线上,CA切圆O于A点,∠ACB的平分线CD交AE于点F,交AB于点D.

    (1)求∠ADF的度数;

    (2)若AB=AC,求AC∶BC.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图所示,已知圆O外有一点P,作圆O的切线PM,M为切点,过PM的中点N,作割线NAB,交圆于A、B两点,连接PA并延长,交圆O于点C,连接PB交圆O于点D,若MC=BC.

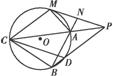
    (1)求证:△APM∽△ABP;

    (2)求证:四边形PMCD是平行四边形.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)=2sin(ωx+),x∈R,其中ω>0,-π<≤π.若f(x)的最小正周期为6π,且当x=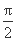时,f(x)取得最大值,则(　　)

    (A)f(x)在区间[-2π,0]上是增函数

    (B)f(x)在区间[-3π,-π]上是增函数

    (C)f(x)在区间[3π,5π]上是减函数

    (D)f(x)在区间[4π,6π]上是减函数

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    双曲线-=1的离心率为　    . 

    查看答案和解析>>

    同步练习册答案