
如图,☉O和☉O′相交于A,B两点,过A作两圆的切线分别交两圆于C、D两点,连结DB并延长交☉O于点E.证明:

(1)AC·BD=AD·AB;
(2)AC=AE.
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:
如图,直线AB为圆的切线,切点为B,点C在圆上,∠ABC的角平分线BE交圆于点E,DB垂直BE交圆于点D.

(1)证明:DB=DC;
(2)设圆的半径为1,BC= ,延长CE交AB于点F,求△BCF外接圆的半径.
,延长CE交AB于点F,求△BCF外接圆的半径.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图所示,PC与圆O相切于点C,直线PO交圆O于A,B两点,弦CD垂直AB于E,则下面结论中,错误的结论是( )

(A)△BEC∽△DEA
(B)∠ACE=∠ACP
(C)DE2=OE·EP
(D)PC2=PA·AB
查看答案和解析>>
科目:高中数学 来源: 题型:
设双曲线C的中心为点O,若有且只有一对相交于点O,所成的角为60°的直线A1B1和A2B2,使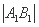 =
=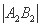 ,其中A1,B1和A2,B2分别是这对直线与双曲线C的交点,则该双曲线的离心率的取值范围是( )
,其中A1,B1和A2,B2分别是这对直线与双曲线C的交点,则该双曲线的离心率的取值范围是( )
(A) 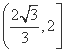 (B)
(B) 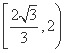
(C) 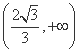 (D)
(D) 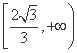
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com