
【题目】已知函数![]() ,其中
,其中![]() 是实数。设
是实数。设![]() ,
, ![]() 为该函数图象上的两点,且
为该函数图象上的两点,且![]() .
.
(1)若函数![]() 的图象在点
的图象在点![]() 处的切线互相垂直,且
处的切线互相垂直,且![]() ,求
,求![]() 的最小值;
的最小值;
(2)若函数![]() 的图象在点
的图象在点![]() 处的切线重合,求
处的切线重合,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)利用导数的几何意义即可得到切线的斜率,因为切线互相垂直,可得![]() ,即
,即![]() .可得
.可得![]() ,再利用基本不等式的性质即可得出;(2)当
,再利用基本不等式的性质即可得出;(2)当![]() 或
或![]() 时,∵
时,∵![]() ,故不成立,∴
,故不成立,∴![]() ,分别写出切线的方程,根据两条直线重合的充要条件
,分别写出切线的方程,根据两条直线重合的充要条件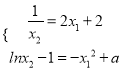 即可得出
即可得出![]() ,记
,记![]() 再利用导数即可得出.
再利用导数即可得出.
试题解析:(1)由导数的几何意义可知,点![]() 处的切线斜率为
处的切线斜率为![]() ,点
,点![]() 处的切线斜率为
处的切线斜率为![]() ,故当
,故当![]() 处的切线与
处的切线与![]() 处的切线垂直时,
处的切线垂直时, ![]() ,当
,当![]() 时,有
时,有![]() ,所以
,所以![]() ,
, ![]() ,所以
,所以![]() ,所以
,所以![]() ,当且仅当
,当且仅当![]() ,即
,即![]() ,
, ![]() 时,等号成立,所以
时,等号成立,所以![]() 的最小值为
的最小值为![]() .
.
(2)当![]() 或
或![]() 时,
时, ![]() ,所以
,所以![]() ,当
,当![]() 时,函数
时,函数![]() 图象在点
图象在点![]() 处的切线方程为
处的切线方程为![]() ,即
,即![]() ,当
,当![]() 时,函数
时,函数![]() 图象在点
图象在点![]() 处的切线方程为
处的切线方程为![]() ,即
,即![]() ,两处切线重合的充要条件是
,两处切线重合的充要条件是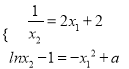 ,由
,由![]() 及
及![]() ,得
,得![]() ,
, ![]() ,记
,记![]() ,则
,则![]() ,所以
,所以![]() 在
在![]() 单调递减,
单调递减, ![]() ,
, ![]() 趋近于
趋近于![]() 时,
时, ![]() 趋近于
趋近于![]() ,所以
,所以![]() ,所以
,所以![]() 的取值范围是
的取值范围是![]() .
.


 走进文言文系列答案
走进文言文系列答案科目:高中数学 来源: 题型:
【题目】已知抛物线 ![]() 的焦点为F,直线
的焦点为F,直线 ![]() 与x轴的交点为P,与抛物线的交点为Q,且
与x轴的交点为P,与抛物线的交点为Q,且 ![]() .
.
(1)求抛物线的方程;
(2)过F的直线l与抛物线相交于A,D两点,与圆 ![]() 相交于B,C两点(A,B两点相邻),过A,D两点分别作抛物线的切线,两条切线相交于点M,求△ABM与△CDM的面积之积的最小值.
相交于B,C两点(A,B两点相邻),过A,D两点分别作抛物线的切线,两条切线相交于点M,求△ABM与△CDM的面积之积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(cosx)-x与函数g(x)=cos(sinx)-x在区间(0, ![]() )都为减函数,设x1,x2,x3∈(0,
)都为减函数,设x1,x2,x3∈(0, ![]() ),且cosx1=x1 , sin(cosx2)=x2 , cos(sinx3)=x3 , 则x1,x2,x3的大小关系是( )
),且cosx1=x1 , sin(cosx2)=x2 , cos(sinx3)=x3 , 则x1,x2,x3的大小关系是( )
A.x1<x2<x3
B.x3<x1<x2
C.x2<x1<x3
D.x2<x3<x1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)已知函数![]() ,
,![]() (
( ![]() 为常数).
为常数).
(1)求函数![]() 在点 (
在点 (![]() ,
,![]() )处的切线方程;
)处的切线方程;
(2)当![]() 时,设
时,设![]() ,若函数
,若函数![]() 在定义域上存在单调减区间,求实数
在定义域上存在单调减区间,求实数![]() 的取值范围;
的取值范围;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解人们对于国家新颁布的“生育二胎放开”政策的热度,现在某市进行调查,随机调查了![]() 人,他们年龄大点频数分布及支持“生育二胎”人数如下表:
人,他们年龄大点频数分布及支持“生育二胎”人数如下表:
年龄 |
|
|
|
|
|
| ||
频数 |
|
|
|
|
|
| ||
支持“生育二胎” |
|
|
|
|
|
| ||
(Ⅰ)由以上统计数据填下面 | 年龄不低于 | 年龄低于 | 合计 | |||||
支持 |
|
| ||||||
不支持 |
|
| ||||||
合计 | ||||||||
(Ⅱ)若对年龄在![]() 的的被调查人中随机选取两人进行调查,恰好这两人都支持“生育二胎放开”的概率是多少?
的的被调查人中随机选取两人进行调查,恰好这两人都支持“生育二胎放开”的概率是多少?
参考数据: ![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
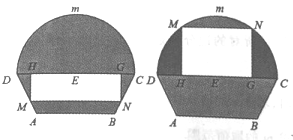
【题目】如图所示的自动通风设施.该设施的下部![]() 是等腰梯形,其中
是等腰梯形,其中![]() 为2米,梯形的高为1米,
为2米,梯形的高为1米, ![]() 为3米,上部
为3米,上部![]() 是个半圆,固定点
是个半圆,固定点![]() 为
为![]() 的中点.
的中点. ![]() 是由电脑控制可以上下滑动的伸缩横杆(横杆面积可忽略不计),且滑动过程中始终保持和
是由电脑控制可以上下滑动的伸缩横杆(横杆面积可忽略不计),且滑动过程中始终保持和![]() 平行.当
平行.当![]() 位于
位于![]() 下方和上方时,通风窗的形状均为矩形
下方和上方时,通风窗的形状均为矩形![]() (阴影部分均不通风).
(阴影部分均不通风).
(1)设![]() 与
与![]() 之间的距离为
之间的距离为![]() (
(![]() 且
且![]() )米,试将通风窗的通风面积
)米,试将通风窗的通风面积![]() (平方米)表示成关于
(平方米)表示成关于![]() 的函数
的函数![]() ;
;
(2)当![]() 与
与![]() 之间的距离为多少米时,通风窗的通风面积
之间的距离为多少米时,通风窗的通风面积![]() 取得最大值?
取得最大值?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com