
【题目】已知等差数列![]() 满足
满足![]() ,
,![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() 满足
满足![]() .
.
(Ⅰ)求![]() 和
和![]() 的通项公式;
的通项公式;
(Ⅱ)若![]() ,
,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() ,
,![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】
(Ⅰ)根据题设条件,列出方程组求得![]() 的值,即可得到得出数列
的值,即可得到得出数列![]() 的通项公式,再利用数列的递推关系,得到数列
的通项公式,再利用数列的递推关系,得到数列![]() 是首项为1,公比为2的等比数列,即可求出数列的通项公式;
是首项为1,公比为2的等比数列,即可求出数列的通项公式;
(Ⅱ)由(Ⅰ)可得![]() ,利用乘公比错位相减法,即可求解.
,利用乘公比错位相减法,即可求解.
(Ⅰ)设等差数列![]() 的公差为
的公差为![]() ,
,
因为![]() ,
,![]() ,可得
,可得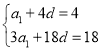 ,解得
,解得![]() ,
,
所以![]() ,
,
对于数列![]() ,当
,当![]() 时,
时,![]() ,解得
,解得![]() .
.
当![]() 时,
时,![]() ,
,![]() ,
,
两式相减,得![]() ,即
,即![]() ,
,
所以![]() 是以1为首项,2为公比的等比数列,所以
是以1为首项,2为公比的等比数列,所以![]() .
.
(Ⅱ)由(Ⅰ)可得![]() .
.
令![]() ,
,
当![]() 时,
时,![]() .
.
当![]() 时,
时,![]() ,
,
则![]() .
.
两式相减,得![]()
![]() ,
,
得![]() ,而
,而![]() 时也符合该式,所以
时也符合该式,所以![]() ,
,
故题中不等式可化为![]() .(*),
.(*),
当![]() 时,不等式(*)可化为
时,不等式(*)可化为![]() ,解得
,解得![]() ;
;
当![]() 时,不等式(*)可化为
时,不等式(*)可化为![]() ,此时
,此时![]() ;
;
当![]() 时,不等式(*)可化为
时,不等式(*)可化为![]() ,因为数列
,因为数列![]() 是递增数列,所以
是递增数列,所以![]() ,
,
综上,实数![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】程大位是明代著名数学家,他的《新编直指算法统宗》是中国历史上一部影响巨大的著作.它问世后不久便风行宇内,成为明清之际研习数学者必读的教材,而且传到朝鲜、日本及东南亚地区,对推动汉字文化圈的数学发展起了重要的作用.卷八中第33问是:“今有三角果一垛,底阔每面七个,问该若干?”如图是解决该问题的程序框图.执行该程序框图,求得该垛果子的总数![]() 为( )
为( )
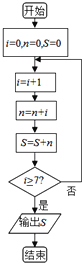
A.84B.56C.35D.28
查看答案和解析>>
科目:高中数学 来源: 题型:
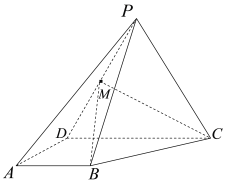
【题目】如图,在四棱锥![]() 中,等边三角形
中,等边三角形![]() 所在的平面垂直于底面
所在的平面垂直于底面![]() ,
,![]() ,
, ![]() ,
,![]() 是棱
是棱![]() 的中点.
的中点.
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)判断直线![]() 与平面
与平面![]() 的是否平行,并说明理由.
的是否平行,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在以ABCDEF为顶点的五面体中,底面ABCD为菱形,∠ABC=120°,AB=AE=ED=2EF,EF![]() AB,点G为CD中点,平面EAD⊥平面ABCD.
AB,点G为CD中点,平面EAD⊥平面ABCD.
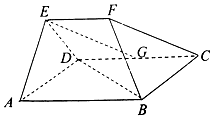
(1)证明:BD⊥EG;
(2)若三棱锥![]() ,求菱形ABCD的边长.
,求菱形ABCD的边长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 的参数方程为
的参数方程为 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,上顶点为
,上顶点为![]() ,
,![]() 的面积为1,且椭圆
的面积为1,且椭圆![]() 的离心率为
的离心率为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)点![]() 在椭圆上且位于第二象限,过点
在椭圆上且位于第二象限,过点![]() 作直线
作直线![]() ,过点
,过点![]() 作直线
作直线![]() ,若直线
,若直线![]() 的交点
的交点![]() 恰好也在椭圆
恰好也在椭圆![]() 上,求点
上,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了解家长对学校食堂的满意情况,分别从高一、高二年级随机抽取了20位家长的满意度评分,其频数分布表如下:
满意度评分分组 |
|
|
|
|
| 合计 |
高一 | 1 | 3 | 6 | 6 | 4 | 20 |
高二 | 2 | 6 | 5 | 5 | 2 | 20 |
根据评分,将家长的满意度从低到高分为三个等级:
满意度评分 | 评分 | 70 | 评分 |
满意度等级 | 不满意 | 满意 | 非常满意 |
假设两个年级家长的评价结果相互独立,根据所给数据,以事件发生的频率作为相应事件发生的概率.现从高一、高二年级各随机抽取1名家长,记事件![]() :“高一家长的满意度等级高于高二家长的满意度等级”,则事件
:“高一家长的满意度等级高于高二家长的满意度等级”,则事件![]() 发生的概率为__________.
发生的概率为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分13分)
某食品厂进行蘑菇的深加工,每公斤蘑菇的成本20元,并且每公斤蘑菇的加工费为![]() 元(
元(![]() 为常数,且
为常数,且![]() ,设该食品厂每公斤蘑菇的出厂价为
,设该食品厂每公斤蘑菇的出厂价为![]() 元(
元(![]() ),根据市场调查,销售量
),根据市场调查,销售量![]() 与
与![]() 成反比,当每公斤蘑菇的出厂价为30元时,日销售量为100公斤.
成反比,当每公斤蘑菇的出厂价为30元时,日销售量为100公斤.
(Ⅰ)求该工厂的每日利润![]() 元与每公斤蘑菇的出厂价
元与每公斤蘑菇的出厂价![]() 元的函数关系式;
元的函数关系式;
(Ⅱ)若![]() ,当每公斤蘑菇的出厂价
,当每公斤蘑菇的出厂价![]() 为多少元时,该工厂的利润
为多少元时,该工厂的利润![]() 最大,并求最大值.
最大,并求最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com