
湛江为建设国家卫生城市,现计划在相距20 km的赤坎区(记为A)霞山区(记为B)两城区外以AB为直径的半圆弧 上选择一点C建造垃圾处理厂,其对市区的影响度与所选地
上选择一点C建造垃圾处理厂,其对市区的影响度与所选地
点到市区的距离有关,对赤坎区和霞山区的总影响度为两市区的影响度之和,记C点到赤坎区的距离为x km,建在C处的垃圾处理厂对两市区的总影响度为y.统计调查表明:垃圾处理厂对赤坎区的影响度与所选地点到赤坎区的距离的平方成反比,比例系数为4;对霞山区的影响度与所选地点到霞山区的距离的平方成反比,比例系数为k.当垃圾处理厂建在 的中点时,对两市区的总影响度为0.065.
的中点时,对两市区的总影响度为0.065.
(1)将y表示成x的函数;
(2)讨论(1)中函数的单调性,并判断 上是否存在一点,使建在此处的垃圾处理厂对城A和城B的总影响度最小?若存在,求出该点到赤坎区的距离;若不存在,说明理由.
上是否存在一点,使建在此处的垃圾处理厂对城A和城B的总影响度最小?若存在,求出该点到赤坎区的距离;若不存在,说明理由.
(1)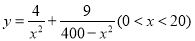 ;(2)
;(2)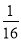 .
.
【解析】
试题分析:(1)根据条件中描述:垃圾处理厂对赤坎区的影响度与所选地点到赤坎区的距离的平方成反比,比例系数为4;对霞山区的影响度与所选地点到霞山区的距离的平方成反比,比例系数为k,而y表示建在C处的垃圾处理厂对两市区的总影响度为y,因此可设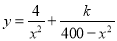 ,根据题意当垃圾处理厂建在
,根据题意当垃圾处理厂建在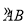 的中点时,对两市区的总影响度为0.065可求得k的值;(2)由(1),
的中点时,对两市区的总影响度为0.065可求得k的值;(2)由(1),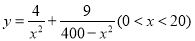 ,可求得
,可求得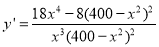 ,进而可以得到y的在(0,20)上的单调性,从而求得y的最小值.
,进而可以得到y的在(0,20)上的单调性,从而求得y的最小值.
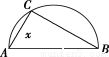
(1)如图,由题意知AC⊥BC,AC=x km,则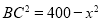 ,
,
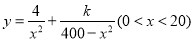 2分
2分
由题意知,当垃圾处理厂建在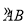 的中点时,对城A和城B的总影响度为0.065,即当
的中点时,对城A和城B的总影响度为0.065,即当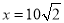 时,y=0.065,代入
时,y=0.065,代入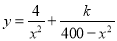 得k=9.所以y表示成x的函数为
得k=9.所以y表示成x的函数为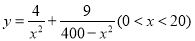 . 6分;
. 6分;
(2)由于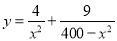 ,∴
,∴ 8分
8分
令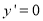 得
得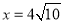 或
或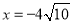 (舍去), 9分
(舍去), 9分
当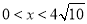 时,
时,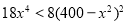 ,即
,即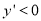 ,此时函数为单调减函数;当
,此时函数为单调减函数;当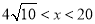 时,
时,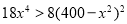 ,即
,即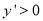 ,此时函数为单调增函数 12分
,此时函数为单调增函数 12分
所以当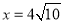 时,即当C点到赤坎区的距离为
时,即当C点到赤坎区的距离为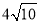 时,函数
时,函数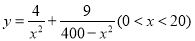 有最小值
有最小值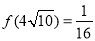 14分.
14分.
考点:1、具体情境下函数解析式的求解;2、利用导数判断函数的单调性求最值.


科目:高中数学 来源:2015届广东省高二下学期第二次月考理科数学卷(解析版) 题型:选择题
设 分别是定义在
分别是定义在 上的奇函数和偶函数,当
上的奇函数和偶函数,当 时,
时, ,
,
且 ,则不等式
,则不等式 的解集是( )
的解集是( )
A. B.
B.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2015届广东省珠海市高三9月摸底考试理科数学试卷(解析版) 题型:选择题
下列命题中是真命题的是()
A. ,均有
,均有
B.若 为奇函数,则
为奇函数,则
C.命题“ ”为真命题,命题“
”为真命题,命题“ ”为假命题,则命题“
”为假命题,则命题“ ”为假命题
”为假命题
D. 是函数
是函数 的极值点
的极值点
查看答案和解析>>
科目:高中数学 来源:2015届广东省高二下学期中段考理科数学试卷(解析版) 题型:填空题
已知函数f(x)的定义域为[-1,5],部分对应值如表:
x | -1 | 0 | 4 | 5 |
f(x) | 1 | 2 | 2 | 1 |
f(x)的导函数y=f'(x)的图象如图所示:
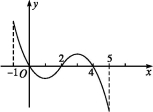
下列关于f(x)的命题:
①函数f(x)是周期函数;
②函数f(x)在[0,2]上是减函数;
③如果当x∈[-1,t]时,f(x)的最大值是2,那么t的最大值为4;
④当1<a<2时,函数y=f(x)-a有4个零点;
⑤函数y=f(x)-a的零点个数可能为0, 1,2,3,4个.
其中正确命题的序号是 .
查看答案和解析>>
科目:高中数学 来源:2015届广东省高二下学期中段考文科数学试卷(解析版) 题型:选择题
某车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了5次试验.
根据收集到的数据(如下表),由最小二乘法求得回归方程
零件数x(个) | 10 | 20 | 30 | 40 | 50 |
加工时间y(min) | 62 | m | n | 81 | 89 |
则m+n的值为:
A.137 B.129 C.121 D.118
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com