Question

3．设向量$\overrightarrow a，\overrightarrow b$满足$|{\overrightarrow a}|=|{\overrightarrow b}|=1，\overrightarrow a•\overrightarrow b=0$，若向量$\overrightarrow c$满足$|{\vec c-\vec a-\vec b}|=1$，则$|{\overrightarrow c}|$的取值范围是（　　）

• A． [$\sqrt{2}$-1，$\sqrt{2}$+1]
• B． [$\sqrt{2}$-1，$\sqrt{2}$+2]
• C． [1，$\sqrt{2}$+1]
• D． [1，$\sqrt{2}$+2]1

Answer 1

分析 由题意知，$\overrightarrow{a}，\overrightarrow{b}$是互相垂直的两个单位向量，在平面直角坐标系中画出图形，由|$\overrightarrow{c}-\overrightarrow{a}-\overrightarrow{b}$|=|$\overrightarrow{c}-（\overrightarrow{a}+\overrightarrow{b}）$|=1，借助几何意义求得答案．

解答 解：∵$|{\overrightarrow a}|=|{\overrightarrow b}|=1，\overrightarrow a•\overrightarrow b=0$，且|$\overrightarrow{c}-\overrightarrow{a}-\overrightarrow{b}$|=|$\overrightarrow{c}-（\overrightarrow{a}+\overrightarrow{b}）$|=1，
∴作出图象如图，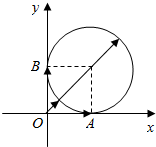

由图可知，$|{\overrightarrow c}|$最小值为$\sqrt{2}-1$，最大值为$\sqrt{2}+1$．
故选：A．

点评 本题考查平面向量的数量积运算，考查了数形结合的解题思想方法，是中档题．