
分析 根据对应函数的图象与性质,即可求出对应函数的极限值.
解答 解:(1)根据反比例函数y=$\frac{1}{x+1}$的图象知,
$\underset{lim}{x→∞}$$\frac{1}{x+1}$=0;
(2)根据指数函数y=3x的图象知,$\underset{lim}{x→∞}$3x不存在;
(3)根据指数函数y=${(\frac{1}{2})}^{x}$的图象知,$\underset{lim}{x→∞}$($\frac{1}{2}$)x=0;
(4)根据正弦函数y=sinx的图象知,$\underset{lim}{x→0}$sinx=sin0=0;
(5)根据正切函数y=tanx的图象知,$\underset{lim}{x→\frac{π}{4}}$tanx=tan$\frac{π}{4}$=1;
(6)根据对数函数y=lnx的图象知,$\underset{lim}{x→1}$lnx=ln1=0.
点评 本题考查了根据函数的图象与性质求极限值的应用问题,是基础题目.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | π | D. | 2π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | π | D. | 2π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
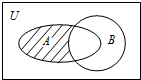 已知全集U=R,集合$A=\{\;x|\;{(\frac{1}{2})^x}≤1\;\}$,B={x|x2-6x+8≤0},则图中阴影部分所表示的集合为( )
已知全集U=R,集合$A=\{\;x|\;{(\frac{1}{2})^x}≤1\;\}$,B={x|x2-6x+8≤0},则图中阴影部分所表示的集合为( )| A. | {x|x≤0} | B. | {x|2≤x≤4} | C. | {x|0<x≤2或x≥4} | D. | {x|0≤x<2或x>4} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com