
 如图,在三棱柱FPE-ACB中,AC=BC=2,∠ACB=90°.△PAB为等边三角形,PC⊥BC.
如图,在三棱柱FPE-ACB中,AC=BC=2,∠ACB=90°.△PAB为等边三角形,PC⊥BC.分析 (Ⅰ)由已知证明△PAC≌△PBC,可得PC⊥CA,再由线面垂直的判定证明平面PBC⊥平面ABC;
(Ⅱ)由题意可得PC=AC=2,取PA中点G,连接BG、CG,则BG⊥PA,CG⊥PA,则∠BGC为二面角B-AP-C的平面角,求解直角三角形可得二面角B-AP-C的正弦值;直接由三棱锥的体积公式求得三棱锥p-ABC的体积.
解答 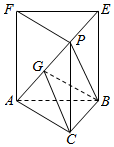 (Ⅰ)证明:如图,∵AC=BC,PA=PB,PC=PC,
(Ⅰ)证明:如图,∵AC=BC,PA=PB,PC=PC,
∴△PAC≌△PBC,
∵PC⊥BC,∴PC⊥CA,
又AC∩BC=C,∴PC⊥面ABC,
∵PC?面PAC,
∴平面PBC⊥平面ABC;
(Ⅱ)解:在Rt△ACB中,由AC=BC=2,得AB=$2\sqrt{2}$,
∵△PAB为等边三角形,∴PA=PB=$2\sqrt{2}$,
在Rt△PCA中,可得PC=2,
取PA中点G,连接BG、CG,则BG⊥PA,CG⊥PA,
∴∠BGC为二面角B-AP-C的平面角,
在Rt△BCG中,由CG=$\sqrt{2}$,BC=2,得$BG=\sqrt{{2}^{2}+(\sqrt{2})^{2}}=\sqrt{6}$,
∴$sin∠BGC=\frac{2}{\sqrt{6}}=\frac{\sqrt{6}}{3}$;
${V}_{P-ABC}=\frac{1}{3}×\frac{1}{2}×2×2×2=\frac{4}{3}$.
点评 本题考查平面与平面垂直的判定,考查了三棱锥体积的求法,考查空间想象能力和思维能力,是中档题.


科目:高中数学 来源:2016-2017学年广东清远三中高二上学期第一次月考数学(理)试卷(解析版) 题型:选择题
平面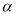 截球
截球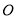 的球面所得圆的半径为
的球面所得圆的半径为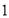 ,球心
,球心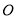 到平面
到平面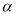 的距离为
的距离为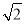 ,则球
,则球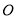 的表面积为( )
的表面积为( )
A. B.
B. C.
C.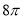 D.
D.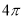
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
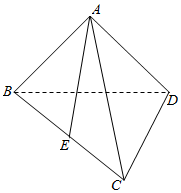 如图,在三棱锥A-BCD中,CD⊥BD,AB=AD,E为BC的中点.
如图,在三棱锥A-BCD中,CD⊥BD,AB=AD,E为BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|0≤x≤3} | B. | {1,2} | C. | {0,1,2} | D. | {0,1,2,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
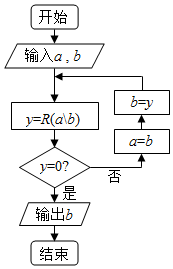 “辗转相除法”的算法思路如图所示,记R(a\b)为a除以b所得的余数(a,b∈N*),执行如图的程序框图,若输入a,b分别为405,75,则输出b的值为( )
“辗转相除法”的算法思路如图所示,记R(a\b)为a除以b所得的余数(a,b∈N*),执行如图的程序框图,若输入a,b分别为405,75,则输出b的值为( )| A. | 3 | B. | 5 | C. | 15 | D. | 25 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com