
| A. | $\frac{1}{2}$ | B. | $\sqrt{2}$ | C. | 2$\sqrt{2}$ | D. | 1 |
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -$\frac{5}{3}$ | C. | -$\frac{1}{3}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
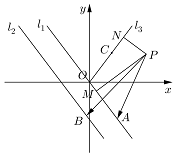 如图,已知直线l1:kx+y=0和直线l2:kx+y+b=0(b>0),射线OC的一个法向量为$\overrightarrow{n_3}$=(-k,1),点O为坐标原点,且k≥0,直线l1和l2之间的距离为2,点A、B分别是直线l1、l2上的动点,P(4,2),PM⊥l1于点M,PN⊥OC于点N;
如图,已知直线l1:kx+y=0和直线l2:kx+y+b=0(b>0),射线OC的一个法向量为$\overrightarrow{n_3}$=(-k,1),点O为坐标原点,且k≥0,直线l1和l2之间的距离为2,点A、B分别是直线l1、l2上的动点,P(4,2),PM⊥l1于点M,PN⊥OC于点N;查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 3 | 4 | 5 | 6 | 7 |
| y | 4 | a+b-4 | -0.5 | 0.5 | -2 |
| A. | 增加1.4个单位 | B. | 减少1.4个单位 | C. | 增加1.2个单位 | D. | 减少1.2个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
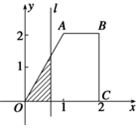 如图,直角梯形OABC中,AB∥OC,|AB|=1,|OC|=|BC|=2,直线l:x=t截此梯形所得位于l左方图形面积为S,则函数S=f(t)的图象大致为图中的( )
如图,直角梯形OABC中,AB∥OC,|AB|=1,|OC|=|BC|=2,直线l:x=t截此梯形所得位于l左方图形面积为S,则函数S=f(t)的图象大致为图中的( )| A. |  | B. | 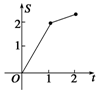 | C. |  | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“?x0∈R,${x_0}^2-{x_0}≤0$”的否定为“?x∈R,x2-x>0” | |
| B. | 命题“在△ABC中,A>30°,则$sinA>\frac{1}{2}$”的逆否命题为真命题 | |
| C. | 若非零向量$\overrightarrow a$、$\overrightarrow b$满足$|{\overrightarrow a+\overrightarrow b}|=|{\overrightarrow a}|-|{\overrightarrow b}|$,则$\overrightarrow a$与$\overrightarrow b$共线 | |
| D. | 设{an}是公比为q的等比数列,则“q>1”是“{an}为递增数列”的充分必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com