
 如图,在△ABC中,∠BAC=60°,AB=3,AC=2,D是BC边上的一点(含端点),则$\overrightarrow{AD}$•$\overrightarrow{BC}$的取值范围是[-6,1].
如图,在△ABC中,∠BAC=60°,AB=3,AC=2,D是BC边上的一点(含端点),则$\overrightarrow{AD}$•$\overrightarrow{BC}$的取值范围是[-6,1]. 分析 建立平面直角坐标系,求出各点坐标,使用坐标计算.
解答 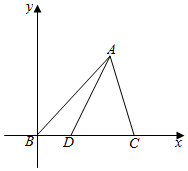 解:以BC所在直线为x轴,以B为原点建立平面直角坐标系,
解:以BC所在直线为x轴,以B为原点建立平面直角坐标系,
∵BC=$\sqrt{A{B}^{2}+A{C}^{2}-2AB•ACcos∠BAC}$=$\sqrt{7}$.∴cosB=$\frac{A{B}^{2}+B{C}^{2}-A{C}^{2}}{2AB•AC}$=$\frac{9+7-4}{6\sqrt{7}}$=$\frac{2}{\sqrt{7}}$.∴sinB=$\frac{\sqrt{3}}{\sqrt{7}}$.
∴A($\frac{6}{\sqrt{7}}$,$\frac{3\sqrt{3}}{\sqrt{7}}$),B(0,0),C($\sqrt{7}$,0).
设D(a,0),则$\overrightarrow{AD}$=(a-$\frac{6}{\sqrt{7}}$,-$\frac{3\sqrt{3}}{\sqrt{7}}$),$\overrightarrow{BC}$=($\sqrt{7}$,0).
∴$\overrightarrow{AD}•\overrightarrow{BC}$=$\sqrt{7}$a-6.
∵D是BC边上的一点(含端点),∴0≤a≤$\sqrt{7}$.
∴当a=0时,$\overrightarrow{AD}•\overrightarrow{BC}$取得最小值-6,当a=$\sqrt{7}$时,$\overrightarrow{AD}•\overrightarrow{BC}$取得最大值1.
故答案为[-6,1].
点评 本题考查了平面向量的数量积运算,建立坐标系是常用方法,属于中档题.


科目:高中数学 来源:2017届浙江嘉兴市高三上学期基础测试数学试卷(解析版) 题型:选择题
对于空间的三条直线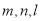 和三个平面
和三个平面 ,则下列命题中为假命题的是( )
,则下列命题中为假命题的是( )
A.若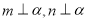 ,则
,则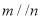
B.若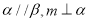 ,则
,则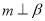
C.若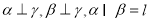 ,则
,则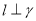
D.若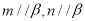 ,则
,则
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ¬p:存在x∈R,使得ex<x | B. | ¬p:任意x∈R,总有ex<x | ||
| C. | ¬p:存在x∈R,使得ex≤x | D. | ¬p:任意x∈R,总有ex≤x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y-4=0 | B. | x-3=0 | C. | y-4=2(x-3) | D. | y-4=x-3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com