
(本小题满分12分)
如图所示的几何体中,四边形ABCD是等腰梯形,AD//CD,  ,FC
,FC  平面ABCD, AE
平面ABCD, AE  BD,CB =CD=-CF.
BD,CB =CD=-CF.
(Ⅰ)求证:平面ABCD  平面AED;
平面AED;
(Ⅱ)直线AF与面BDF所成角的余弦值
(Ⅰ)见解析 (Ⅱ)
解析试题分析:(Ⅰ)通过计算可证得AD⊥BD,又因为AE⊥BD,由线面垂直的判定定理得,BD⊥面ADE,由面面垂直的判定定理得,面ADE⊥面ABCD; (Ⅱ)由(Ⅰ)知AD⊥BD,同理可证AC⊥BC,因为CF⊥面ABCD,所以以CA,CB,CF分别为 建立空间直角坐标系,设BC=1,求出A、B、D,F点的坐标,求出
建立空间直角坐标系,设BC=1,求出A、B、D,F点的坐标,求出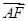 的坐标和平面BDF法向量的坐标,利用空间向量夹角公式计算出这两个向量夹角的余弦值,利用同脚三角函数基本关系求出向量夹角的正弦值即为线面夹角的余弦值.
的坐标和平面BDF法向量的坐标,利用空间向量夹角公式计算出这两个向量夹角的余弦值,利用同脚三角函数基本关系求出向量夹角的正弦值即为线面夹角的余弦值.
试题解析:(Ⅰ)∵四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°,
∴∠ADC=∠BCD=120°,
又CB=CD,∴∠CDB=30°,∴∠ADB=90°,AD⊥BD,
又AE⊥BD,且AE∩AD=A,AE,AD?平面AED,
∴BD⊥平面AED,∴平面ABCD⊥平面AED.
(Ⅱ)连结AC,由(Ⅰ)知AD⊥BD,∴AC⊥BC,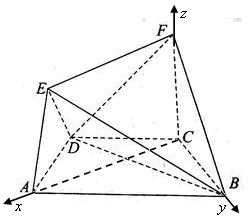
又FC⊥平面ABCD,∴CA,CB,CF两两垂直,
以C为坐标原点,建立空间直角坐标系,设CB=1,
则A( ,0,0),B(0,1,0),D(
,0,0),B(0,1,0),D( ,
,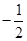 ,0),F(0,0,1),
,0),F(0,0,1),
∴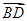 =(
=( ,
,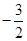 ,0),
,0),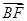 ==(0,?1,1),
==(0,?1,1),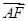 =(-
=(- ,0,1),
,0,1),
设平面BDF的一个法向量为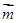 =(x,y,z),则
=(x,y,z),则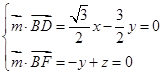 ,取z=1,则
,取z=1,则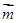 =(
=( ,1,1),
,1,1),
所以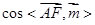 =
=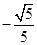 ,∴直线AF与面BDF所成角的余弦值为
,∴直线AF与面BDF所成角的余弦值为 . (12分)
. (12分)
考点:空间线面垂直的判定,空间面面垂直的判定,线面角的计算,推理论证能力,运算求解能力


 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:高中数学 来源: 题型:填空题
下列各命题:
①若直线 ,则
,则 不可能与
不可能与 内无数条直线相交。
内无数条直线相交。
②若平面 内有一条直线和直线
内有一条直线和直线 不共面,则
不共面,则 。
。
③若一个平面内有不共线的三点到另一平面的距离相等,则两平面平行。
④如果两个平面垂直,则一个平面内任意直线都和另一个平面垂直。
其中错误命题的序号是____________.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,点 为斜三棱柱
为斜三棱柱 的侧棱
的侧棱 上一点,
上一点,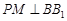 交
交 于点
于点 ,
, 交
交 于点
于点 .
.
(1) 求证: ;
;
(2) 在任意 中有余弦定理:
中有余弦定理: .
.
拓展到空间,类比三角形的余弦定理,写出斜三棱柱的三个侧面面积与其中两个侧面所成的二面角之间的关系式,并予以证明
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在直三棱柱中 -A BC中,AB
-A BC中,AB 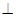 AC, AB=AC=2,
AC, AB=AC=2,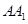 =4,点D是BC的中点.
=4,点D是BC的中点.
(1)求异面直线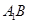 与
与 所成角的余弦值;
所成角的余弦值;
(2)求平面 与
与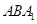 所成二面角的正弦值.
所成二面角的正弦值.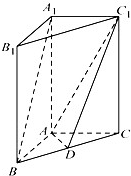
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com