
分析 由已知通过求解三角形得到角B,再由余弦定理求得c,然后代入投影公式得答案.
解答 解:在△ABC中,∵cosA=-$\frac{3}{5}$,∴sinA=$\frac{4}{5}$.
又a=4$\sqrt{2}$,b=5,
由正弦定理,$\frac{a}{sinA}=\frac{b}{sinB}$,得sinB=$\frac{bsinA}{a}=\frac{5×\frac{4}{5}}{4\sqrt{2}}=\frac{\sqrt{2}}{2}$,
由题意可知a>b,即A>B,B=$\frac{π}{4}$,
由余弦定理可知$(4\sqrt{2})^{2}={5}^{2}+{c}^{2}-2×5c×(-\frac{3}{5})$.
解得:c=1,c=-7(舍去).
向量$\overrightarrow{BA}$在$\overrightarrow{BC}$方向上的投影为:|$\overrightarrow{BA}$|cosB=ccosB=$1×\frac{\sqrt{2}}{2}=\frac{\sqrt{2}}{2}$.
故答案为:$\frac{\sqrt{2}}{2}$.
点评 本题考查平面向量的数量积运算,考查了利用正弦定理和余弦定理求解三角形,关键是掌握向量在向量上投影的概念,是中档题.


科目:高中数学 来源: 题型:解答题
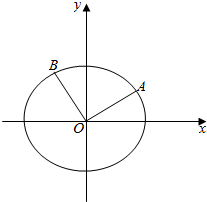 如图,已知点A是单位圆上一点,且位于第一象限,以x轴的正半轴为始边,OA为终边的角设为α,将OA绕坐标原点逆时针旋转$\frac{π}{2}$至OB.
如图,已知点A是单位圆上一点,且位于第一象限,以x轴的正半轴为始边,OA为终边的角设为α,将OA绕坐标原点逆时针旋转$\frac{π}{2}$至OB.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com