
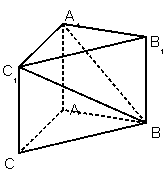
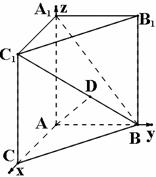
如图,在三棱柱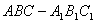 中,
中,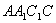 是边长为
是边长为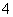 的正方形,平面
的正方形,平面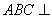 平面
平面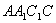 ,
,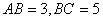 .
.
(1)求证: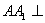 平面
平面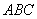 ;
;
(2)求二面角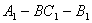 的余弦值;
的余弦值;
 (3)证明:在线段
(3)证明:在线段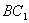 上存在点
上存在点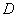 ,使得
,使得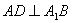 ,并求
,并求 的值。
的值。
解:(I)因为AA1C1C为正方形,所以AA1 ⊥AC.
因为平面ABC⊥平面AA1C1C,且AA1垂直于这两个平面的交线AC,
所以AA1⊥平面ABC.……… 3分
(II)由(I)知AA1 ⊥AC,AA1 ⊥AB. 由题知AB=3,BC=5,AC=4,所以AB⊥AC. 如图,以A为原点建立空间直角坐标系A-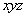 ,则B(0,3,0),A1(0,0,4),B1(0,3,4),C1(4,0,4),
,则B(0,3,0),A1(0,0,4),B1(0,3,4),C1(4,0,4),
设平面A1BC1的法向量为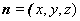 ,则
,则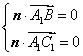 ,即
,即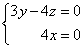 ,
,
令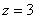 ,则
,则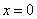 ,
,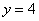 ,所以
,所以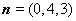 .……… 6分
.……… 6分
同理可得,平面BB1C1的法向量为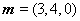 ,所以
,所以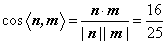 . 由题知二面角A1-BC1-B1为锐角,所以二面角A1-BC1-B1的余弦值为
. 由题知二面角A1-BC1-B1为锐角,所以二面角A1-BC1-B1的余弦值为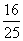 .……… 8分
.……… 8分
(III)设D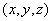 是直线BC1上一点,且
是直线BC1上一点,且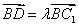 . 所以
. 所以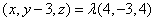 .解得
.解得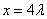 ,
,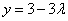 ,
,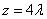 .
.
所以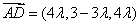 .
.
由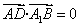 ,即
,即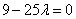 .解得
.解得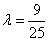 .……… 11分
.……… 11分
因为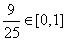 ,所以在线段BC1上存在点D,
,所以在线段BC1上存在点D,
使得AD⊥A1B.
 此时,
此时,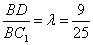 .……… 13分
.……… 13分


科目:高中数学 来源: 题型:
在某种新型材料的研制中,实验人员获得了右边一组实验数据:现准备用下列四个函数中的一个近似地表示这些数据的规律,其中最接近的一个是
( )
|
| 1.99 | 3 | 4 | 5.1 | 6.12 |
|
| 1.5 | 4.04 | 7.5 | 12 | 18.01 |
A. 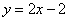 B.
B. 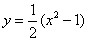
B.C.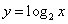 D.
D. 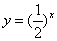
查看答案和解析>>
科目:高中数学 来源: 题型:
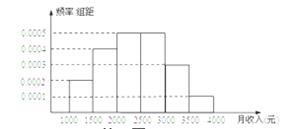
一个社会调查机构就某地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(如上图)。为了分析居民的收入与年龄、学历、职业等方面的关系,要从这10000人中再用分层抽样方法抽出100人作进一步调查,则在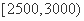 (元)月收入段应抽出
(元)月收入段应抽出
的人数为( ).
A.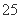 B.
B.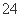 C.
C.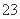 D.
D.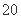
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com