
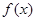
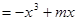 在
在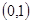 上是增函数,
上是增函数,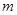 的取值集合
的取值集合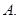 ;
;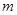 取值集合
取值集合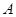 中的最小值时,定义数列
中的最小值时,定义数列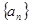 ;满足
;满足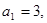 且
且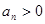 ,
,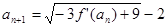 ,求数列
,求数列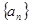 的通项公式;
的通项公式;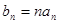 ,数列
,数列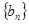 的前
的前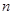 项和为
项和为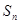 ,求证:
,求证: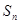
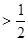 .
.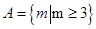 ;(2)
;(2)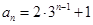 ;(3)详见解析
;(3)详见解析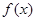 在区间
在区间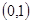 是增函数,说明
是增函数,说明 恒成立,再参变分离确定
恒成立,再参变分离确定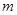 的取值集合
的取值集合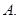 ;
;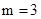 ,表示
,表示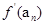 ,代入
,代入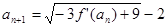 中,得关于
中,得关于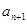 和
和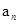 的递推式,再根据递推公式求通项公式,常见的根据递推公式求通项公式的方法有:①
的递推式,再根据递推公式求通项公式,常见的根据递推公式求通项公式的方法有:① ,用累积法;②
,用累积法;②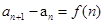 ,用累加法;③
,用累加法;③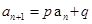 (p,q是常数),用构造法;④
(p,q是常数),用构造法;④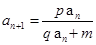 (p,q,m是常数),用两边取倒数,再用构造法,该题
(p,q,m是常数),用两边取倒数,再用构造法,该题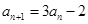 ,用③求
,用③求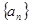 ;(3)首先求数列
;(3)首先求数列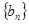 的通项公式,再根据通项公式的具体形式,选择合适的求和方法,常见的求和方法有①直接法,直接利用等比数列或等差数列前n项和公式;②裂项相消法,在求和的过程中互相抵消的办法;③错位相减法,适合于通项公式是等差数列乘以等比数列的类型;④分组求和法,分组分别求和再相加的办法;⑤奇偶并项求和法,研究奇数项和偶数项的特点来求和的办法,该题
的通项公式,再根据通项公式的具体形式,选择合适的求和方法,常见的求和方法有①直接法,直接利用等比数列或等差数列前n项和公式;②裂项相消法,在求和的过程中互相抵消的办法;③错位相减法,适合于通项公式是等差数列乘以等比数列的类型;④分组求和法,分组分别求和再相加的办法;⑤奇偶并项求和法,研究奇数项和偶数项的特点来求和的办法,该题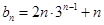 ,利用③④结合起来求和,再证明不等式成立.
,利用③④结合起来求和,再证明不等式成立.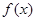 在
在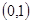 上是增函数,只需
上是增函数,只需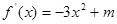 在
在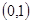 满足
满足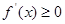 恒成立,即
恒成立,即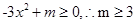 ,所以
,所以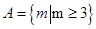 ;
;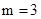 ,因为
,因为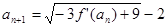 ,∴
,∴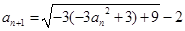 ,且
,且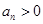 ,所以
,所以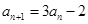 ,∴
,∴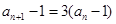 ,∴
,∴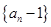 是以2为首项,3为公比的等比数列,故
是以2为首项,3为公比的等比数列,故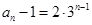 ,
,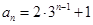 ;
;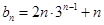 ,令
,令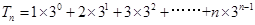 ,
,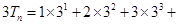
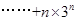 ,两式相减得
,两式相减得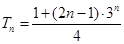 ,故
,故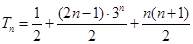
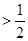 .
.

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:解答题
 为函数
为函数 图象上一点,
图象上一点, 为坐标原点,记直线
为坐标原点,记直线 的斜率
的斜率 .
. 在区间
在区间 上存在极值,求实数
上存在极值,求实数 的取值范围;
的取值范围; 时,不等式
时,不等式 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
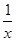 -a
-a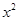 +x(a>0).
+x(a>0).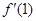 =
=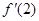 ,求f(x)图像在x=1处的切线的方程;
,求f(x)图像在x=1处的切线的方程;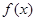 的极大值和极小值分别为m,n,证明:
的极大值和极小值分别为m,n,证明: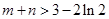 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com