练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知向量．

    (1)若分别表示将一枚质地均匀的正方体骰子（六个面的点数分别为1,2,3,4,5,6）先后抛掷两次时第一次、第二次出现的点数，求满足的概率；

    (2)若在连续区间上取值，求满足的概率.

    【答案】（1）；（2）．

    【解析】

    试题分析：(1)本题为古典概型问题.基本事件共个,满足即的基本事件有,由此可得结论；(2)由题意知,本题为几何概型问题,且概率为面积比.

    试题解析：(1)将一枚质地均匀的正方体骰子先后抛掷两次，所包含的基本事件总数为个...............1分

    由有

    所以满足的基本事件为，共3个..............3分

    故满足的概率为...............5分；

    (2)若在连续区间上取值，则全部基本事件的结果为...............6分

    满足的基本事件的结果为..............8分

    画出图形如图，矩形面积为25

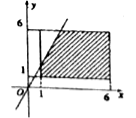
    阴影部分面积为...............11分

    故满足的概率为...............12分.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】一青蛙从点开始依次水平向右和竖直向上跳动，其落点坐标依次是，（如图所示，坐标以已知条件为准），表示青蛙从点到点所经过的路程．

    （1）若点为抛物线（）准线上一点，点均在该抛物线上，并且直线经过该抛物线的焦点，证明．

    （2）若点要么落在所表示的曲线上，要么落在所表示的曲线上，并且,试写出（不需证明）；

    （3）若点要么落在所表示的曲线上，要么落在所表示的曲线上，并且，求的表达式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，其中.

    （I）讨论函数的单调性；

    （II）若，证明：对任意 ，总有.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，，其中且，.

    （I）若，且时，的最小值是－2,求实数的值；

    （II）若，且时，有恒成立，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】的内角的对边分别为，已知

    (1)求；

    (2)若，求面积的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

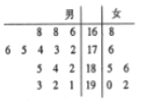
    【题目】公司从某大学招收毕业生，经过综合测试，录用了名男生和名女生，这名毕业生的测试成绩如茎叶图所示（单位：分），公司规定：成绩在分以上者到甲部门工作；分以下者到乙部门工作，另外只有成绩高于分才能担任助理工作。

    （1）如果用分层抽样的方法从甲部门人选和乙部门人选中选取人，再从这人中选人，那么至少有一人是甲部门人选的概率是多少？

    （2）若从所有甲部门人选中随机选人，用表示所选人员中能担任助理工作的男生人数，写出的分布列，并求出的数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数为奇函数

    （1）比较的大小，并说明理由.（提示： ）

    （2）若，且对恒成立，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆内有一点为过点且倾斜角为的弦．

    （1）当时，求弦的长；

    （2）当弦被平分时，圆经过点且与直线相切于点，求圆的标准方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2009年推出一种新型家用轿车，购买时费用为万元，每年应交付保险费、养路费及汽油费共万元，汽车的维修费为：第一年无维修费用，第二年为万元，从第三年起，每年的维修费均比上一年增加万元.（1）设该辆轿车使用年的总费用（包括购买费用、保险费、养路费、汽油费及维修费）为，求的表达式；（2）这种汽车使用多少年报废最合算（即该车使用多少年，年平均费用最少）？

    查看答案和解析>>

    同步练习册答案