
分析 (1)函数$f(x)=a+\frac{1}{{{4^x}+1}}$为定义在R上的奇函数.则f(0)=0,解得a的值;
(2)证法一:任取x1,x2∈(-∞,+∞),且x1<x2,作差判断f(x2)与f(x1)的大小,结合单调性的定义,可得函数f(x)在(-∞,+∞)的单调性;
证法二:求导,判断导函数的符号,进而可得函数f(x)在(-∞,+∞)的单调性.
解答 解:(1)∵函数$f(x)=a+\frac{1}{{{4^x}+1}}$为定义在R上的奇函数.
∴f(0)=0,…(2分)
即$a+\frac{1}{{{4^0}+1}}=0$,解得$a=-\frac{1}{2}$.…(4分)
(2)由(1)知$a=-\frac{1}{2}$,则$f(x)=\frac{1}{2}+\frac{1}{{{4^x}+1}}$,…(5分)
函数f(x)在(-∞,+∞)上单调递减,给出如下证明:…(6分)
证法一:任取x1,x2∈(-∞,+∞),且x1<x2,…(7分)
则$f({x_2})-f({x_1})=(\frac{1}{2}+\frac{1}{{{4^{x_2}}+1}})-$$(\frac{1}{2}+\frac{1}{{{4^{x_1}}+1}})$
=$\frac{1}{{{4^{x_2}}+1}}-$$\frac{1}{{{4^{x_1}}+1}}$=$\frac{{{4^{x_1}}-{4^{x_2}}}}{{({4^{x_1}}+1)({4^{x_2}}+1)}}$…(9分)
=$\frac{{{4^{x_1}}(1-{4^{{x_2}-{x_1}}})}}{{({4^{x_1}}+1)({4^{x_2}}+1)}}$,…(10分)
∵x1<x2,∴x2-x1>0,∴${4^{{x_2}-{x_1}}}>1$,∴$1-{4^{{x_2}-{x_1}}}>0$,…(11分)
又∵${4^{x_1}}>0$,${4^{x_1}}+1>0$,${4^{x_2}}+1>0$,
∴$\frac{{{4^{x_1}}(1-{4^{{x_2}-{x_1}}})}}{{({4^{x_1}}+1)({4^{x_2}}+1)}}$>0,即f(x2)-f(x1)>0,
∴f(x2)>f(x1),
∴函数f(x)在(-∞,+∞)上单调递减.…(12分)
证法二:∵$f(x)=\frac{1}{2}+\frac{1}{{{4^x}+1}}$
∴$f′(x)=\frac{-ln4•{4}^{x}}{{(4}^{x}+1)^{2}}$,…(9分)
∵f′(x)<0恒成立,…(11分)
故函数f(x)在(-∞,+∞)上单调递减.…(12分)
点评 本题考查的知识点是函数的单调性的判断与证明,函数的奇偶性,是函数图象和性质的综合应用,难度中档.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
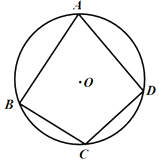
| A. | 2 | B. | 4 | C. | $\sqrt{3}$ | D. | $2\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①或③ | B. | ①或② | C. | ②或③ | D. | ①或②或③ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com