
| A. | y=|sinx| | B. | y=tan|x| | C. | y=cosx | D. | y=-cosx |
分析 根据正弦函数、余弦函数的单调性,正切函数的定义域,以及偶函数的定义便可判断每个选项的正误,从而找出正确选项.
解答 解:A.x∈(0,π)时,y=|sinx|=sinx;
sinx在(0,π)上没有单调性,∴该选项错误;
B.x=$\frac{π}{2}$时,y=tanx无意义,∴该选项错误;
C.y=cosx在(0,π)上单调递减,∴该选项错误;
D.y=-cosx的定义域为R,且-cos(-x)=-cosx;
∴该函数为偶函数;
y=cosx在(0,π)上单调递减,∴y=-cosx在(0,π)上单调递增,∴该选项正确.
故选D.
点评 考查正弦函数、余弦函数的单调性,函数单调性的定义,以及正切函数的定义域,偶函数的定义.


科目:高中数学 来源: 题型:选择题
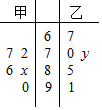 一次数学考试后,某老师从自己带的两个班级中各抽取5人,记录他们的考试成绩,得到如图所示的茎叶图,已知甲班5名同学成绩的平均数为81,乙班5名同学的中位数为73,则x-y的值为( )
一次数学考试后,某老师从自己带的两个班级中各抽取5人,记录他们的考试成绩,得到如图所示的茎叶图,已知甲班5名同学成绩的平均数为81,乙班5名同学的中位数为73,则x-y的值为( )| A. | 2 | B. | -2 | C. | 3 | D. | -3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
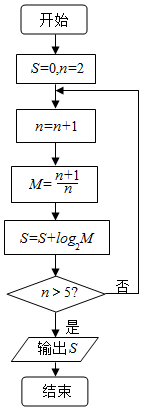
| A. | 1 | B. | log2$\frac{6}{5}$ | C. | log2$\frac{7}{3}$ | D. | log23 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{97}{100}$ | B. | $\frac{99}{100}$ | C. | $\frac{100}{101}$ | D. | $\frac{102}{101}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com