
用数学归纳法证明an+1+(a+1)2n-1能被a2+a+1整除(n∈N*).
证明:① 当n=1时,a2+(a+1)=a2+a+1可被a2+a+1整除.
② 假设n=k(k∈N*)时,ak+1+(a+1)2k-1能被a2+a+1整除,则当n=k+1时,ak+2+(a+1)2k+1=a·ak+1+(a+1)2(a+1)2k-1=a·ak+1+a·(a+1)2k-1+(a2+a+1)(a+1)2k-1=a[ak+1+(a+1)2k-1]+(a2+a+1)(a+1)2k-1,由假设可知a[ak+1+(a+1)2k-1]能被a2+a+1整除,(a2+a+1)(a+1)2k-1也能被a2+a+1整除,∴ ak+2+(a+1)2k+1能被a2+a+1整除,即n=k+1时命题也成立,
∴ 对任意n∈N*原命题成立.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:高中数学 来源: 题型:
已知椭圆C: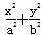 =1(a>b>0)经过点M(-2,-1),离心率为
=1(a>b>0)经过点M(-2,-1),离心率为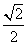 .过点M作倾斜角互补的两条直线分别与椭圆C交于异于M的另外两点P、Q.
.过点M作倾斜角互补的两条直线分别与椭圆C交于异于M的另外两点P、Q.
(1) 求椭圆C的方程;
(2) 试判断直线PQ的斜率是否为定值,证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
若等差数列{an}的公差为d,前n项的和为Sn,则数列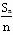 为等差数列,公差为
为等差数列,公差为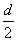 .类似地,若各项均为正数的等比数列{bn}的公比为q,前n项的积为Tn,则数列{
.类似地,若各项均为正数的等比数列{bn}的公比为q,前n项的积为Tn,则数列{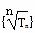 }为等比数列,公比为________.
}为等比数列,公比为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
设数列{an}:1,-2,-2,3,3,3,-4,-4,-4,-4,…,(-1)k-1k,…, 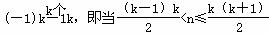 (k∈N*)时,an=(-1)k-1k,记Sn=a1+a2+…+an(n∈N*),用数学归纳法证明Si(2i+1)=-i(2i+1)(i∈N*).
(k∈N*)时,an=(-1)k-1k,记Sn=a1+a2+…+an(n∈N*),用数学归纳法证明Si(2i+1)=-i(2i+1)(i∈N*).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com