
 已知过点A(-1,0)的动直线l与圆C:x2+(y-3)2=4相交于P、Q两点,l与直线m:x+3y+6=0相交于N.
已知过点A(-1,0)的动直线l与圆C:x2+(y-3)2=4相交于P、Q两点,l与直线m:x+3y+6=0相交于N.分析 (1)根据直线m的一个法向量为(1,3),求得直线l的一个方向向量,由此求得l的点向式方程,可得直线l过圆心.
(2)由|PQ|=2$\sqrt{3}$得圆心C到直线l的距离d=1,设直线l的方程为x-ny+1=0,求得n的值,可得直线l的方程.
解答 解:(1)因为l与m垂直,直线m的一个法向量为(1,3),
所以直线l的一个方向向量为$\overrightarrow{d}$=(1,3),所以l的方程为$\frac{x+1}{1}=\frac{y}{3}$,即3x-y+3=0.
所以直线l过圆心C(0,3).
(2)由|PQ|=2$\sqrt{3}$,得圆心C到直线l的距离d=1,
设直线l的方程为x-ny+1=0,则由d=$\frac{|1-3n|}{\sqrt{1+{n}^{2}}}$=1.
解得n=0,或n=$\frac{3}{4}$,
所以直线l的方程为x+1=0或4x-3y+4=0.
点评 本题主要考查两条直线垂直的性质,点到直线的距离公式,两个向量坐标形式的运算,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | f($\frac{π}{4}$)=-1 | B. | f(x)的周期为$\frac{π}{2}$ | C. | ω的最大值为4 | D. | f($\frac{3π}{4}$)=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{4}$ | B. | -$\frac{5}{6}$ | C. | 1 | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,e3-4] | B. | [0,$\frac{1}{{e}^{3}}$+2] | C. | [$\frac{1}{{e}^{3}}$+2,e3-4] | D. | [e3-4,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{5}+1}{2}$ | D. | $\frac{\sqrt{3}+1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | -1 | C. | 1 | D. | $\frac{{\sqrt{3}-1}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
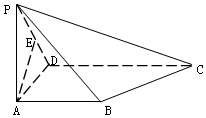 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AB∥CD,∠ADC=90°,$AD=AB=\frac{1}{2}CD=1$,PA⊥平面ABCD,E为PD中点,且PC⊥AE.
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AB∥CD,∠ADC=90°,$AD=AB=\frac{1}{2}CD=1$,PA⊥平面ABCD,E为PD中点,且PC⊥AE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com