
 如图,已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为直角梯形,∠D=90°,且AB∥CD,AB=AD,∠BCD=45°.
如图,已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为直角梯形,∠D=90°,且AB∥CD,AB=AD,∠BCD=45°.分析 (1)取PD的中点M,连接FM,AM.推导出四边形ABFM为平行四边形,从而BF∥AM,由此求出当F为线段PC中点时,BF∥平面PAD.
(2)以A点为原点,AB,AD,AP所在直线为x,y,z轴建立空间直角坐标系,利用向量法能求出二面角B-PC-D的大小.
解答 解:(1)当F为PC的中点时,BF∥平面PAD.(2分)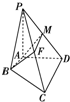
证明如下:
取PD的中点M,连接FM,AM.
由AB=AD,∠BCD=45°,得AB=$\frac{1}{2}$CD=FM.
又FM∥CD∥AB,
所以四边形ABFM为平行四边形,所以BF∥AM.(4分)
又AM?平面PAD,BF?平面PAD,
所以BF∥平面PAD.(6分)
(2)由题意知AB,AD,AP两两垂直,
则以A点为原点,AB,AD,AP所在直线为x,y,z轴建立空间直角坐标系.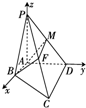
由题意∠PBA为直线PB与平面ABCD所成的角,则∠PBA=45°,所以PA=AB.
设PA=AB=AD=1,则A(0,0,0),B(1,0,0),D(0,1,0),C(2,1,0),P(0,0,1),
$\overrightarrow{PB}$=(1,0,-1),$\overrightarrow{PC}$=(2,1,-1),$\overrightarrow{PD}$=(0,1,-1).(8分)
设平面PBC的法向量为$\overrightarrow{n}$=(x,y,z),则$\overrightarrow{PB}$?$\overrightarrow{n}$=0,$\overrightarrow{PC}$?$\overrightarrow{n}$=0,
∴$\left\{\begin{array}{l}{x-z=0}\\{2x+y-z=0}\end{array}\right.$,令z=1,得$\overrightarrow{n}$=(1,-1,1).(10分)
同理可以求出平面PCD的法向量$\overrightarrow{m}$=(0,1,1),
∵$\overrightarrow{n}•\overrightarrow{m}$=0,
∴平面PBC⊥平面PCD,即二面角B-PC-D为90°.(12分)
点评 本查满足线面平行的点的位置的确定与求法,考查二面角的求法,是中档题,解题时要认真审题,注意向量法的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | (-1,0) | B. | (-∞,-1)∪(0,1) | C. | (-1,1) | D. | (0,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
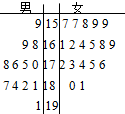 第26届世界大学生夏季运动会将于2011年8月12日到23日在深圳举行,为工作需要,组委会拟定组建一个“五人接待小组”,先在各中学进行海选,招募了12名男生和18名女生志愿者,将这30名志愿者的身高编成如图所示的茎叶图(单位:cm).若身高
第26届世界大学生夏季运动会将于2011年8月12日到23日在深圳举行,为工作需要,组委会拟定组建一个“五人接待小组”,先在各中学进行海选,招募了12名男生和18名女生志愿者,将这30名志愿者的身高编成如图所示的茎叶图(单位:cm).若身高查看答案和解析>>
科目:高中数学 来源: 题型:解答题
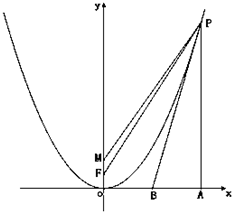 已知点P(x0,y0)(x0≠0)是抛物线x2=2y上的一动点,F为焦点,点M的坐标为(0,1).
已知点P(x0,y0)(x0≠0)是抛物线x2=2y上的一动点,F为焦点,点M的坐标为(0,1).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(a)<0,f(b)<0 | B. | f(a)>0,f(b)>0 | C. | f(a)<0,f(b)>0 | D. | f(a)>0,f(b)<0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | (-1,∞)∪(2,+∞) | C. | (-∞,2) | D. | (-∞,1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com