
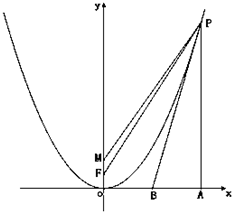
 已知点P(x0,y0)(x0≠0)是抛物线x2=2y上的一动点,F为焦点,点M的坐标为(0,1).
已知点P(x0,y0)(x0≠0)是抛物线x2=2y上的一动点,F为焦点,点M的坐标为(0,1).分析 (Ⅰ)求出圆的圆心与半径,利用圆的圆心与半径,半弦长满足勾股定理,列出方程即可求证:以MP为直径的圆截直线$y=\frac{1}{2}$所得的弦长为定值;
(Ⅱ)求出函数的导数,得到切线方程,求出B的坐标,求出点B到直线PA的距离为${d_1}=\frac{{|{x_0}|}}{2}$,求直线PF的方程,点B到直线PF的距离为${d_2}=\frac{{|{({x_0^2-1})\frac{x_0}{2}+{x_0}}|}}{{\sqrt{{{({x_0^2-1})}^2}+{{({2{x_0}})}^2}}}}=\frac{{|{x_0}|}}{2}$,推出结果.
解答 解:(Ⅰ)以MP为直径的圆的圆心为$({\frac{x_0}{2},\frac{1}{2}{y_0}+\frac{1}{2}})$,
$|{MP}|=\sqrt{x_0^2+{{({{y_0}-1})}^2}}=\sqrt{2{y_0}+{{({{y_0}-1})}^2}}=\sqrt{y_0^2+1}$,----------(5分)
所以圆的半径$r=\frac{1}{2}\sqrt{y_0^2+1}$,
圆心到直线$y=\frac{1}{2}$的距离$d=|{\frac{1}{2}{y_0}+\frac{1}{2}-\frac{1}{2}}|=|{\frac{1}{2}{y_0}}|$;
故截得的弦长$l=2\sqrt{{r^2}-{d^2}}=2\sqrt{\frac{1}{4}y_0^2+\frac{1}{4}-\frac{1}{4}y_0^2}=1$----------(10分)
(Ⅱ)因为$y=\frac{x^2}{2},y'=x,{k_l}={y^'}{|_{x={x_0}}}={x_0}$,
所以切线l的方程为$y-\frac{x_0^2}{2}={x_0}(x-{x_0})$,即$y={x_0}x-\frac{x_0^2}{2}$
令y=0,得$x=\frac{x_0}{2}$,所以点B的坐标为 $B(\frac{x_0}{2},0)$----------(12分)
点B到直线PA的距离为${d_1}=\frac{{|{x_0}|}}{2}$,
下面求直线PF的方程.
因为$F(0,\frac{1}{2})$,所以直线PF的方程为$y-\frac{1}{2}=\frac{{\frac{x_0^2}{2}-\frac{1}{2}}}{x_0}(x-0)$,
整理得$({x_0^2-1})x-2{x_0}y+{x_0}=0$
所以点B到直线PF的距离为${d_2}=\frac{{|{({x_0^2-1})\frac{x_0}{2}+{x_0}}|}}{{\sqrt{{{({x_0^2-1})}^2}+{{({2{x_0}})}^2}}}}=\frac{{|{x_0}|}}{2}$,
所以d1=d2
所以直线PB是∠APF的平分线----------(15分)
点评 本题考查直线与抛物线的位置关系的应用,函数的导数以及切线方程的求法,考查转化思想以及计算能力.


 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案科目:高中数学 来源: 题型:解答题
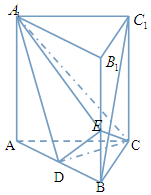 如图,在直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB=$\frac{{\sqrt{2}}}{2}$AB.
如图,在直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB=$\frac{{\sqrt{2}}}{2}$AB.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
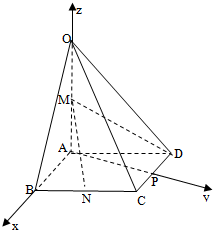 如图,在四棱锥O-ABCD中,底面ABCD是菱形,∠ABC=60°,OA=AB=2,OA⊥底面ABCD,M为OA的中点,N为BC的中点.作AP⊥CD于点P,分别以AB,AP,AO所在直线为x,y,z轴,建立如图空间直角坐标系.
如图,在四棱锥O-ABCD中,底面ABCD是菱形,∠ABC=60°,OA=AB=2,OA⊥底面ABCD,M为OA的中点,N为BC的中点.作AP⊥CD于点P,分别以AB,AP,AO所在直线为x,y,z轴,建立如图空间直角坐标系.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为直角梯形,∠D=90°,且AB∥CD,AB=AD,∠BCD=45°.
如图,已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为直角梯形,∠D=90°,且AB∥CD,AB=AD,∠BCD=45°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{32}{3}π$ | B. | 16π | C. | 144π | D. | 288π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com