
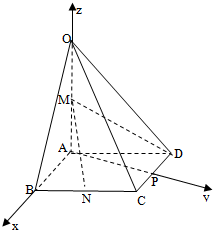
 如图,在四棱锥O-ABCD中,底面ABCD是菱形,∠ABC=60°,OA=AB=2,OA⊥底面ABCD,M为OA的中点,N为BC的中点.作AP⊥CD于点P,分别以AB,AP,AO所在直线为x,y,z轴,建立如图空间直角坐标系.
如图,在四棱锥O-ABCD中,底面ABCD是菱形,∠ABC=60°,OA=AB=2,OA⊥底面ABCD,M为OA的中点,N为BC的中点.作AP⊥CD于点P,分别以AB,AP,AO所在直线为x,y,z轴,建立如图空间直角坐标系.分析 (1)根据空间直角坐标系,写出对应点与向量的坐标,利用平面OCD的法向量证明MN∥平面OCD;
(2)利用向量的数量积求出AB与MD所成角的余弦值;
(3)利用向量$\overrightarrow{OB}$在法向量上的投影的绝对值求出点B到平面OCD的距离.
解答 解:(1)根据空间直角坐标系得,
A(0,0,0),B(2,0,0),$P(0{,^{\;}}\sqrt{3}{,^{\;}}0)$,$D(-1{,^{\;}}\sqrt{3}{,^{\;}}0)$,
O(0,0,2),M(0,0,1),$N(\frac{3}{2}{,^{\;}}\frac{{\sqrt{3}}}{2}{,^{\;}}0)$,…(2分)
∴$\overrightarrow{MN}=(\frac{3}{2}{,^{\;}}\frac{{\sqrt{3}}}{2}{,^{\;}}-1)$,
$\overrightarrow{OP}=(0{,^{\;}}\sqrt{3}{,^{\;}}-2)$,
$\overrightarrow{OD}=(-1{,^{\;}}\sqrt{3}{,^{\;}}-2)$,…(3分)
设平面OCD的法向量为$\overrightarrow n=(x{,^{\;}}y{,^{\;}}z)$,
则$\overrightarrow n•\overrightarrow{OP}=0$,$\overrightarrow n•\overrightarrow{OD}=0$,
即$\left\{\begin{array}{l}\sqrt{3}y-2z=0\\-x+\sqrt{3}y-2z=0\end{array}\right.$,
取$y=\sqrt{3}$,解得$\overrightarrow n=(0{,^{\;}}\sqrt{3}{,^{\;}}\frac{3}{2})$;…(4分)
$\overrightarrow{MN}$•$\overrightarrow{n}$=($\frac{3}{2}$,$\frac{\sqrt{3}}{2}$,-1)•(0,$\sqrt{3}$,$\frac{3}{2}$)=0,
∴MN∥平面OCD;…(6分)
(2)设AB与MD所成的角为θ,
∵$\overrightarrow{AB}=(2{,^{\;}}0{,^{\;}}0)$,$\overrightarrow{MD}=(-1{,^{\;}}\sqrt{3}{,^{\;}}-1)$,…(7分)
∴$cosθ=\frac{{|\overrightarrow{AB}•\overrightarrow{MD|}}}{{|\overrightarrow{AB}|•|\overrightarrow{MD}|}}=\frac{2}{{2×\sqrt{5}}}=\frac{{\sqrt{5}}}{5}$,…(9分)
∴AB与MD所成角的余弦值为$\frac{{\sqrt{5}}}{5}$;…(10分)
(3)设点B到平面OCD的距离为d,则
d为向量$\overrightarrow{OB}$在向量$\overrightarrow n=(0{,^{\;}}\sqrt{3}{,^{\;}}\frac{3}{2})$上的投影的绝对值,
由$\overrightarrow{OB}=(2{,_{\;}}0{,^{\;}}-2)$,得
$d=\frac{{|\overrightarrow{OB}•\overrightarrow{n|}}}{{|\overrightarrow{n|}}}=\frac{3}{{\frac{{\sqrt{21}}}{2}}}=\frac{{2\sqrt{21}}}{7}$;…(12分)
所以点B到平面OCD的距离为$\frac{{2\sqrt{21}}}{7}$.…(14分)
点评 本题主要考查了空间中的平行和垂直关系的应用问题,也考查了建立空间坐标系,利用向量法求夹角和距离的应用问题,是综合性题目.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | -2k | B. | 0 | C. | 2k | D. | 4k |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
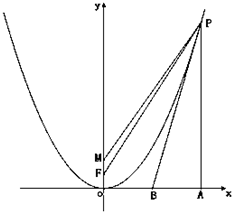 已知点P(x0,y0)(x0≠0)是抛物线x2=2y上的一动点,F为焦点,点M的坐标为(0,1).
已知点P(x0,y0)(x0≠0)是抛物线x2=2y上的一动点,F为焦点,点M的坐标为(0,1).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| P(K2≥k) | 0.10 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com