
分析 (1)先求出an=4n-1,再求A1,A4,A6,A9;
(2)求出数列的通项,利用错位相减法求数列{bn}的前n项和Tn;
(3)${A_{\;i}}=\left\{\begin{array}{l}6{d^2}\;(\;i\;为偶数\;)\\-3{d^2}\;(\;i\;为奇数且\;i≠6m-1,m∈{N^*}\;)\\-12{d^2}\;(\;i=6m-1,m∈{N^*}\;)\end{array}\right.$,分类讨论,即可研究λ的所有可能值,并指出取到每个值时的条件.
解答 解:(1)当n≥2时,an=Sn-Sn-1=4n-1.
∵a1=S1=3符合上式,∴an=4n-1.
∴A1=-48,A4=96,A6=96,A9=-48;
(2)A3=$|\begin{array}{l}{{a}_{4}}&{{a}_{5}}\\{{a}_{7}}&{{a}_{8}}\end{array}|$=(a1+3d)(a1+7d)-(a1+4d)(a1+6d)=-27=-3d2,
∴d=3.
∴an=3n+2,∴${b_n}=\frac{3n+2}{2^n}.\\{T_n}=\frac{1}{2}×5+{(\frac{1}{2})^2}×8+{(\frac{1}{2})^3}×11+…+{(\frac{1}{2})^n}×(3n+2)\;①\\ 2{T_n}=1×5+(\frac{1}{2})×8+{(\frac{1}{2})^2}×11+…+{(\frac{1}{2})^{n-1}}×(3n+2)②\end{array}$
∴Tn=5•$\frac{1}{2}$+8•$\frac{1}{{2}^{2}}$+…+(3n+2)•$\frac{1}{{2}^{n}}$①
∴$\frac{1}{2}$Tn=5•$\frac{1}{{2}^{2}}$+8•$\frac{1}{{2}^{3}}$+…+(3n+2)•$\frac{1}{{2}^{n+1}}$②
$②-①,得\;{T_n}=8-{(\frac{1}{2})^n}×(3n+8)$.
(3)${A_{\;i}}=\left\{\begin{array}{l}6{d^2}\;(\;i\;为偶数\;)\\-3{d^2}\;(\;i\;为奇数且\;i≠6m-1,m∈{N^*}\;)\\-12{d^2}\;(\;i=6m-1,m∈{N^*}\;)\end{array}\right.$
①当i=6m-1,m∈N*时,Ai=$\left\{\begin{array}{l}{-({A}_{i-k}+{A}_{i+k})(k为奇数)}\\{2({A}_{i-k}+{A}_{i+k})(k为偶数,且k≠6p)}\\{\frac{1}{2}({A}_{i-k}+{A}_{i+k})(k=6p)}\end{array}\right.$,∴λ=-1,2,$\frac{1}{2}$;
②i=6m+4或i=6m+6,Ai=$\left\{\begin{array}{l}{\frac{1}{2}({A}_{i-k}+{A}_{i+k})(k为偶数)}\\{-({A}_{i-k}+{A}_{i+k})(k=6p+3)}\\{-\frac{2}{5}({A}_{i-k}+{A}_{i+k})(k=6p+1,6p+5)}\end{array}\right.$,∴λ=-$\frac{2}{5}$,-1,$\frac{1}{2}$;
③i=6m+2,Ai=$\left\{\begin{array}{l}{\frac{1}{2}({A}_{i-k}+{A}_{i+k})(k为偶数)}\\{-({A}_{i-k}+{A}_{i+k})(k为奇数,k≠6p+3)}\\{-\frac{1}{4}({A}_{i-k}+{A}_{i+k})(k=6p+3)}\end{array}\right.$,∴λ=-$\frac{1}{4}$,-1,$\frac{1}{2}$;
④i=6m+1或i=6m+3,Ai=$\left\{\begin{array}{l}{-\frac{1}{4}({A}_{i-k}+{A}_{i+k})(k为奇数)}\\{\frac{1}{2}({A}_{i-k}+{A}_{i+k})(k=6p)}\\{\frac{1}{5}({A}_{i-k}+{A}_{i+k})(k=6p+2或k=6p+4)}\end{array}\right.$,∴λ=-$\frac{1}{4}$,$\frac{1}{5}$,$\frac{1}{2}$,
综上所述,λ取值集合为{-1,2,$\frac{1}{2}$,-$\frac{1}{4}$,$\frac{1}{5}$,-$\frac{2}{5}$}.
点评 本题考查矩阵与数列的结合,考查数列的通项与求和,考查分类讨论的数学思想,难度大.


科目:高中数学 来源: 题型:选择题
| A. | -$\frac{4}{5}$ | B. | -$\frac{3}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | sinα>sinb | B. | log2a<log2b | C. | a3<b3 | D. | ($\frac{1}{2}$)a<($\frac{1}{2}$)b |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在如图所示的几何体中,四边形ABCD是等腰梯形,AB∥CD,AB=2CB=2,∠ABC=60°,在梯形ACEF中,EF∥AC,且AC=2EF=2EC,EC⊥平面ABCD.
在如图所示的几何体中,四边形ABCD是等腰梯形,AB∥CD,AB=2CB=2,∠ABC=60°,在梯形ACEF中,EF∥AC,且AC=2EF=2EC,EC⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
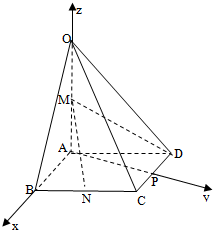 如图,在四棱锥O-ABCD中,底面ABCD是菱形,∠ABC=60°,OA=AB=2,OA⊥底面ABCD,M为OA的中点,N为BC的中点.作AP⊥CD于点P,分别以AB,AP,AO所在直线为x,y,z轴,建立如图空间直角坐标系.
如图,在四棱锥O-ABCD中,底面ABCD是菱形,∠ABC=60°,OA=AB=2,OA⊥底面ABCD,M为OA的中点,N为BC的中点.作AP⊥CD于点P,分别以AB,AP,AO所在直线为x,y,z轴,建立如图空间直角坐标系.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com