
分析 (1)利用对数定义得出$\frac{x+5}{x-5}$>0求解,
(2)根据求函数定义判断.
(3)利用反函数定义求解得出${10^y}=\frac{x+5}{x-5}$∴${f^{-1}}(x)=\frac{{5({{10}^x}+1)}}{{{{10}^x}-1}}(x≠0)$
(4)根据函数单调性转化为不等式求解,注意定义域的限制.
解答 解:(1)∵$\frac{x+5}{x-5}>0$∴定义域为{x|x>5或x<-5};
(2)$f(-x)=lg\frac{-x+5}{-x-5}=lg\frac{x-5}{x+5}=lg{(\frac{x+5}{x-5})^{-1}}=-lg\frac{x+5}{x-5}=-f(x)$
∴f(x)为奇函数;
(3)∵${10^y}=\frac{x+5}{x-5}$∴${f^{-1}}(x)=\frac{{5({{10}^x}+1)}}{{{{10}^x}-1}}(x≠0)$
(4)f(x)>0,
$\frac{x+5}{x-5}$>0∴定义域为{x|x>5或x<-5}
∴$\frac{x+5}{x-5}$>1,解得x>5.
∴x>5
点评 本题综合考察了对数函数的定义,单调性,不等式的运用,属于较简单的综合题目.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
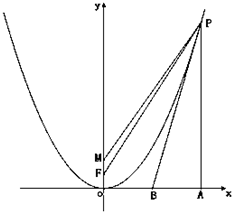 已知点P(x0,y0)(x0≠0)是抛物线x2=2y上的一动点,F为焦点,点M的坐标为(0,1).
已知点P(x0,y0)(x0≠0)是抛物线x2=2y上的一动点,F为焦点,点M的坐标为(0,1).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(a)<0,f(b)<0 | B. | f(a)>0,f(b)>0 | C. | f(a)<0,f(b)>0 | D. | f(a)>0,f(b)<0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| P(K2≥k) | 0.10 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com