Question

4．m，n，l表示三条不同的直线，α，β，γ表示三个不同的平面，下列命题中
①若m，n与l都垂直，则m∥n；
②若m∥α，m∥n，则n∥α；
③若m⊥α，n∥β且α∥β，则m⊥n；
④若γ⊥α，γ⊥β，则α∥β
其中正确的命题是③．（写出所有正确命题的序号）

Answer 1

分析 由m，n，l表示不同直线，α，β，γ表示三个不同平面，知：①若m，n与l都垂直，则m与n平行，相交或异面，从而进行判断；②若m∥α，m∥n，则n∥α或n?α，从而进行判断；③若m⊥α，n∥β且α∥β，则m⊥n成立，从而进行判断；④列举反例即可．

解答 解：m，n，l表示不同直线，α，β，γ表示三个不同平面，
对于①，∵若m⊥l，n⊥l，则m与n平行，相交或异面，故①错误；
对于②，若m∥α，m∥n，则n∥α或n?α，故②不正确；
对于③，由于n∥β且α∥β可得出n?α或n∥α，又m⊥α可得出m⊥n，故若m⊥α，n∥β且α∥β，则m⊥n，故③正确；
④α⊥γ，β⊥γ，如图：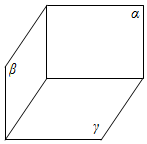

显然此时α与β相交，故④错误． 
故答案为：③．

点评 本题考查命题的真假判断与应用，着重考查空间中直线与平面之间的位置关系及平面与平面之间的位置关系，属于中档题．