
分析 先根据圆C1的方程找出圆心坐标与半径R的值,找出圆C2的半径的最大时的情况:当圆c2的圆心Q为线段AB的中点时,圆c2与圆C1相切,切点在圆C1的劣弧AB上,设切点为P,此时圆C2的半径r的最大,利用距离公式求出两圆心的距离OQ等于d,然后根据两圆内切时,两圆心之间的距离等于两半径相减可得圆C2的半径最大值.
解答 解:由圆C1:x2+y2=9,可得圆心O(0,0),半径R=3
如图,当圆c2的圆心Q为线段AB的中点时,圆c2与圆C1相切,切点在圆C1的劣弧AB上,设切点为P,此时圆C2的半径r的最大.
则两圆心之间的距离OQ=d=$\frac{5}{\sqrt{{3}^{2}+{4}^{2}}}=1$.
因为两圆内切,所以圆c2的最大半径r=3-d=3-1=2
故答案为:2
点评 此题考查学生掌握两圆内切时两半径所满足的条件,灵活运用韦达定理及两点间的距离公式化简求值,是一道中档题.


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
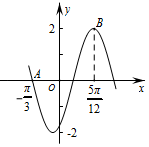 函数f(x)=Asin(ωx+ϕ),($A>0,ω>0,-\frac{π}{2}<ϕ<\frac{π}{2}$)的部分 图象如图所示,则函数f(x)的解析式为f(x)=2sin(2x$-\frac{π}{3}$).
函数f(x)=Asin(ωx+ϕ),($A>0,ω>0,-\frac{π}{2}<ϕ<\frac{π}{2}$)的部分 图象如图所示,则函数f(x)的解析式为f(x)=2sin(2x$-\frac{π}{3}$).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com