
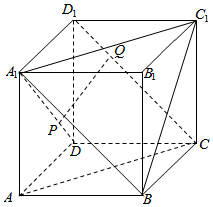
| A. | 在CD1上存在点Q,使得PQ∥平面AA1C1C | |
| B. | 在CD1上存在点Q,使得PQ⊥平面AA1C1C | |
| C. | 在CD1上存在点Q,使得PQ∥平面A1BC1 | |
| D. | 在CD1上存在点Q,使得PQ⊥平面A1BC1 |
分析 过P作PM⊥AD于M,过Q作QN⊥CD于N,连结MN,则当MN∥AC时,平面PMNQ∥平面AA1C1C,故PQ∥平面平面AA1C1C.
解答 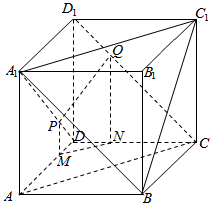 解:当D1Q=$\frac{1}{3}$D1C时,过P作PM⊥AD于M,过Q作QN⊥CD于N连结MN,
解:当D1Q=$\frac{1}{3}$D1C时,过P作PM⊥AD于M,过Q作QN⊥CD于N连结MN,
则$\frac{DM}{DA}=\frac{PD}{D{A}_{1}}=\frac{1}{3}$,$\frac{CN}{CD}=\frac{CQ}{C{D}_{1}}=\frac{2}{3}$,∴$\frac{DN}{DC}=\frac{1}{3}$.
∴$\frac{DM}{DA}=\frac{DN}{DC}$,
∴MN∥AC,又PM∥A1A,PM?平面PMNQ,MN?平面PMNQ,AA1?平面AA1C1C,AC?平面AA1C1C,PM∩MN=M,A1A∩AC=A,
∴平面PMNQ∥平面AA1C1C,
∵PQ?平面PMNQ,
∴PQ∥平面平面AA1C1C
故选:A.
点评 本题考查了线面位置关系的判断,构造平行线或平行平面是判断的关键.


科目:高中数学 来源: 题型:选择题
| A. | 58 | B. | 62 | C. | 238 | D. | 242 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({1,\sqrt{2}})$ | B. | $({1,\sqrt{2}}]$ | C. | $({\sqrt{2},+∞})$ | D. | $[{\sqrt{2},+∞})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,四面体ABCD中,AB=DC=1,BD=$\sqrt{2}$,AD=BC=$\sqrt{3}$,二面角A-BD-C的平面角的大小为60°,E,F分别是BC,AD的中点,则异面直线EF与AC所成的角的余弦值是( )
如图,四面体ABCD中,AB=DC=1,BD=$\sqrt{2}$,AD=BC=$\sqrt{3}$,二面角A-BD-C的平面角的大小为60°,E,F分别是BC,AD的中点,则异面直线EF与AC所成的角的余弦值是( )| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{6}}{3}$ | D. | $\frac{2\sqrt{2}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | 3 | D. | $\frac{\sqrt{5}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
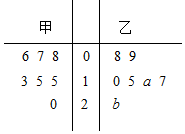 甲、乙两家快餐店对某日7个时段光顺的客人人数进行统计并绘制茎叶图如图所示(下面简称甲数据、乙数据),且乙数据的众数为17,甲数据的平均数比乙数据平均数少2.
甲、乙两家快餐店对某日7个时段光顺的客人人数进行统计并绘制茎叶图如图所示(下面简称甲数据、乙数据),且乙数据的众数为17,甲数据的平均数比乙数据平均数少2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{3}{2}$ | B. | $\frac{3}{2}$ | C. | -6 | D. | 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com