
【题目】已知函数![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)当![]() 时, 若存在区间
时, 若存在区间![]() ,使
,使![]() 在
在![]() 上的值域是
上的值域是![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)当![]() 时,
时, ![]() 在
在![]() 上为减函数, 当
上为减函数, 当![]() 时,
时,![]() 在
在![]() 上为减函数, 在
上为减函数, 在![]() 上为增函数;(2)
上为增函数;(2)![]() .
.
【解析】
试题分析:(1)求![]() ,对
,对![]() 分类讨论解
分类讨论解![]() 可得
可得![]() 的单调性;(2)本题转化为
的单调性;(2)本题转化为![]() 在
在![]() 上至少有两个不同的实数根,通过讨论
上至少有两个不同的实数根,通过讨论![]() ,
,![]() 的单调性得
的单调性得![]() .
.
试题解析:(1)函数![]() 定义域是
定义域是![]() ,
,![]() ,当
,当![]() 时,
时,![]() 在
在![]() 上
上
为减函数, 当![]() 时, 令
时, 令![]() ,则
,则![]() ,当
,当![]() 时,
时,![]() 为减函数, 当
为减函数, 当![]() 时,
时,![]() 为增函数,
为增函数,![]() 当
当![]() 时,
时, ![]() 在
在![]() 上为减函数, 当
上为减函数, 当![]() 时,
时,
![]() 在
在![]() 上为减函数, 在
上为减函数, 在![]() 上为增函数.
上为增函数.
(2)当![]() 时,
时,![]() , 由(1)知:
, 由(1)知:![]() 在
在![]() 上为增函数, 而
上为增函数, 而![]() 在
在![]() 上为增函数, 结合
上为增函数, 结合![]() 在
在![]() 上的值域是
上的值域是![]() 知:
知:
![]() ,其中
,其中![]() .则
.则![]() 在
在![]() 上至少有两个不同的实数根.
上至少有两个不同的实数根.
由![]() 得
得![]() ,记
,记![]() ,
,
则![]() ,记
,记![]() ,则
,则![]() ,
,![]() 在
在![]() 上为增函数, 即
上为增函数, 即![]() 在
在![]() 上为增函数, 而
上为增函数, 而![]() ,
,![]() 当
当![]() 时,
时,![]() , 当
, 当![]() 时,
时,![]() ,
,![]() 在
在![]() 上为减函数, 在
上为减函数, 在![]() 上为增函数, 而
上为增函数, 而![]() ,当
,当![]() 时,
时,![]() , 故结合图象得:
, 故结合图象得:![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】用数学归纳法证明当n∈N*时,1+2+22+…+25n-1是31的倍数时,当n=1时原式为( )
A. 1 B. 1+2
C. 1+2+3+4 D. 1+2+22+23+24
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小李参加一种红包接龙游戏:他在红包里塞了12元,然后发给朋友![]() ,如果
,如果![]() 猜中,
猜中,![]() 将获得红包里的所有金额;如果
将获得红包里的所有金额;如果![]() 未猜中,
未猜中,![]() 将当前的红包转发给朋友
将当前的红包转发给朋友![]() ,如果
,如果![]() 猜中,
猜中,![]() 平分红包里的金额;如果
平分红包里的金额;如果![]() 未猜中,
未猜中,![]() 将当前的红包转发给朋友
将当前的红包转发给朋友![]() ,如果
,如果![]() 猜中,
猜中,![]() 和
和![]() 平分红包里的金额;如果
平分红包里的金额;如果![]() 未猜中,红包里的钱将退回小李的账户,设
未猜中,红包里的钱将退回小李的账户,设![]() 猜中的概率分别为
猜中的概率分别为![]() ,且
,且![]() 是否猜中互不影响.
是否猜中互不影响.
(1)求![]() 恰好获得4元的概率;
恰好获得4元的概率;
(2)设![]() 获得的金额为
获得的金额为![]() 元,求
元,求![]() 的分布列;
的分布列;
(3)设![]() 获得的金额为
获得的金额为![]() 元,
元,![]() 获得的金额为
获得的金额为![]() 元,判断
元,判断![]() 所获得的金额的期望能否超过
所获得的金额的期望能否超过![]() 的期望与
的期望与![]() 的期望之和.
的期望之和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对一个容量为N的总体抽取容量为n的样本,当选取简单随机抽样、系统抽样和分层抽样三种不同方法抽取样本时,总体中每个个体被抽中的概率分别为P1,P2,P3,则
A. P1=P2<P3 B. P2=P3<P1 C. P1=P3<P2 D. P1=P2=P3
查看答案和解析>>
科目:高中数学 来源: 题型:
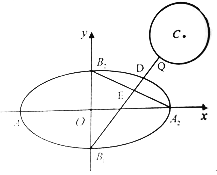
【题目】如图,已知椭圆![]() 的四个顶点分别为
的四个顶点分别为![]() ,左右焦点分别为
,左右焦点分别为![]() ,若圆
,若圆![]() :
:![]() 上有且只有一个点
上有且只有一个点![]() 满足
满足![]() .
.
(1)求圆![]() 的半径
的半径![]() ;
;
(2)若点![]() 为圆
为圆![]() 上的一个动点,直线
上的一个动点,直线![]() 交椭圆于点
交椭圆于点![]() ,交直线
,交直线![]() 于点
于点![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,满足: ①截 y 轴所得弦长为
,满足: ①截 y 轴所得弦长为![]() ; ②被
; ②被![]() 轴分成两段圆弧,其弧长的比为
轴分成两段圆弧,其弧长的比为![]() .
.
(1)求在满足条件①②的所有圆中,使代数式 ![]() 取得最小值时,圆的方程;
取得最小值时,圆的方程;
(2)在(1)中, ![]() 是圆上的任意一点,求
是圆上的任意一点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中正确的是 ( )
A. 任何两个变量都具有相关关系
B. 人的知识与其年龄具有相关关系
C. 散点图中的各点是分散的没有规律
D. 根据散点图求得的回归直线方程都是有意义的
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确的是( ).
A. 若两条直线都平行与同一个平面,则这两条直线平行
B. 过一条直线有且只有一个平面与已知平面垂直
C. 若一条直线平行于一个平面内的一条直线,则这条直线平行于这个平面
D. 若这两条直线垂直于同一个平面,则这两个直线共面
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
为了保护环境,发展低碳经济,某单位在政府部门的支持下,进行技术攻关,采用了新工艺,新上了把二氧化碳转化为一种可利用的化工产品的项目.经测算,月处理成本![]() (元)与月处理量
(元)与月处理量![]() (吨)之间的函数关系可以近似的表示为:
(吨)之间的函数关系可以近似的表示为: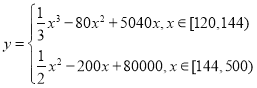 ,且每处理一吨二氧化碳可得到能利用的化工产品价值为200元,若该项目不获利,政府将补贴.
,且每处理一吨二氧化碳可得到能利用的化工产品价值为200元,若该项目不获利,政府将补贴.
(I)当![]() 时,判断该项目能否获利?如果获利,求出最大利润;如果不获利,则政府每月至少需要补贴多少元才能使该项目不亏损;
时,判断该项目能否获利?如果获利,求出最大利润;如果不获利,则政府每月至少需要补贴多少元才能使该项目不亏损;
(II)该项目每月处理量为多少吨时,才能使每吨的平均处理成本最低?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com