
【题目】如图,已知椭圆![]() 的四个顶点分别为
的四个顶点分别为![]() ,左右焦点分别为
,左右焦点分别为![]() ,若圆
,若圆![]() :
:![]() 上有且只有一个点
上有且只有一个点![]() 满足
满足![]() .
.
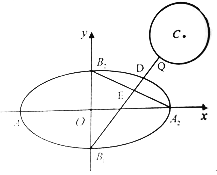
(1)求圆![]() 的半径
的半径![]() ;
;
(2)若点![]() 为圆
为圆![]() 上的一个动点,直线
上的一个动点,直线![]() 交椭圆于点
交椭圆于点![]() ,交直线
,交直线![]() 于点
于点![]() ,求
,求![]() 的最大值.
的最大值.
【答案】(1)半径为![]() ;(2)最大值为
;(2)最大值为![]() .
.
【解析】
试题分析:(1)先由已知条件,求出点![]() 的轨迹方程,再利用两圆相切,求出圆的半径,注意范围;(2)先设出直线
的轨迹方程,再利用两圆相切,求出圆的半径,注意范围;(2)先设出直线![]() 方程
方程![]() ,由直线与圆的位置关系,求出
,由直线与圆的位置关系,求出![]() 的范围,联立直线与圆的方程,求出
的范围,联立直线与圆的方程,求出![]() 点的横坐标, 直线
点的横坐标, 直线![]() 与直线
与直线![]() 的交点为
的交点为![]() 点,求出横坐标,利用相似得出
点,求出横坐标,利用相似得出 ![]() ,代入,再求出范围.
,代入,再求出范围.
试题解析:(1)依题意得,![]() ,设点
,设点![]() ,
,
由![]() 得:
得: ,化简得
,化简得![]() ,
,
∴点![]() 的轨迹是以点
的轨迹是以点![]() 为圆心,
为圆心,![]() 为半径的圆.
为半径的圆.
又∵点![]() 在圆
在圆![]() 上并且有且只有一个点
上并且有且只有一个点![]() ,即两圆相切,
,即两圆相切,
当两圆外切时,圆心距![]() ,成立;
,成立;
当两圆内切时,圆心距![]() ,不成立;
,不成立;
∴![]()
(2)设直线![]() 为
为![]() ,由
,由![]() ,得
,得![]() .
.
联立 消去
消去![]() 并整理得:
并整理得:![]() ,解得点
,解得点![]() 的横坐标为
的横坐标为![]() ,
,
把直线![]() 与直线
与直线![]() :
:![]() 联立解得点
联立解得点![]() 的横坐标为
的横坐标为![]() ,
,
∴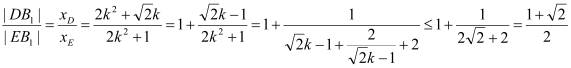
当且仅当![]() 时,取等号,
时,取等号,
∴![]() 的最大值为
的最大值为![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知集合A={x|x2-5x-6<0},B={x|2x<1},则图中阴影部分表示的集合是( )
A. {x|2<x<3} B. {x|-1<x≤0}
C. {x|0≤x<6} D. {x|x<-1}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中,错误的命题是( )
A、平行于同一直线的两个平面平行。
B、一条直线与两个平行平面中的一个相交,那么这条直线必和另一个平面相交。
C、平行于同一平面的两个平面平行。
D、一条直线与两个平行平面所成的角相等。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知椭圆C过点(0,2),其焦点为F1(﹣![]() ,0),F2(
,0),F2(![]() ,0).
,0).
(1)求椭圆C的标准方程;
(2)已知点P在椭圆C上,且PF1=4,求△PF1F2的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一年级要组建数学、计算机、航空模型三个兴趣小组,某同学只选报其中的2个,则基本事件共有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列结论正确的是( )
①函数关系是一种确定性关系;②相关关系是一种非确定性关系;③回归分析是对具有函数关系的两个变量进行统计分析的一种方法;④回归分析是对具有相关关系的两个变量进行统计分析的一种常用方法.
A. ①② B. ①②③ C. ①②④ D. ①②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个年级有20个班,每班都是50人,每个班的学生的学号都是1~50.学校为了了解这个年级的作业量,把每个班中学号为5,15,25,35,45的学生的作业留下,这里运用的是( )
A. 系统抽样 B. 分层抽样 C. 简单随机抽样 D. 随机数表法抽样
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com