
【题目】已知圆![]() ,满足: ①截 y 轴所得弦长为
,满足: ①截 y 轴所得弦长为![]() ; ②被
; ②被![]() 轴分成两段圆弧,其弧长的比为
轴分成两段圆弧,其弧长的比为![]() .
.
(1)求在满足条件①②的所有圆中,使代数式 ![]() 取得最小值时,圆的方程;
取得最小值时,圆的方程;
(2)在(1)中, ![]() 是圆上的任意一点,求
是圆上的任意一点,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() 或
或![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)画出图象,圆心坐标为![]() ,半径为
,半径为![]() ,则点
,则点![]() 到
到![]() 轴,
轴,![]() 轴的距离分别为
轴的距离分别为![]() .利用圆的弦长公式和半径、结合配方法建立方程,进而求出圆心和半径;(2)
.利用圆的弦长公式和半径、结合配方法建立方程,进而求出圆心和半径;(2)![]() 表示的是圆上的点和点
表示的是圆上的点和点![]() 直线连线斜率的取值范围,注意
直线连线斜率的取值范围,注意![]() ,结合图象可知,斜率的取值范围是
,结合图象可知,斜率的取值范围是![]() .
.
试题解析:
(1)如图所示,圆心坐标为 ![]() , 半径为
, 半径为![]() ,则点
,则点![]() 到
到![]() 轴,
轴,![]() 轴的距离分别为
轴的距离分别为![]() .
.
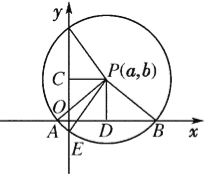
![]() 圆
圆![]() 被
被![]() 轴分成两段圆弧,其弧长的比为
轴分成两段圆弧,其弧长的比为![]() ,
,![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() ,则有
,则有![]() ,取圆
,取圆![]() 截
截![]() 轴的弦的中点
轴的弦的中点![]() ,连接
,连接![]() 圆截
圆截![]() 轴所得弦长为
轴所得弦长为![]() ,
,![]() ,即
,即![]() .则
.则![]() ,
,
![]() 当
当![]() 时,
时,![]() 取得最小值
取得最小值![]() ,此时
,此时![]() ,或
,或![]() .对应的圆为:
.对应的圆为:![]() ,或
,或![]() .
.
(2)因为![]() 由(1)知,
由(1)知,![]() 在
在![]() 一段圆弧上,该圆弧端坐标点为
一段圆弧上,该圆弧端坐标点为![]() 和
和![]()
![]() ,
,![]() 表示
表示![]()
![]() 与
与![]() 连线的斜率,其范围是
连线的斜率,其范围是![]() ,即是
,即是![]() .
.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:高中数学 来源: 题型:
【题目】探索表达式A=(n-1)(n-1)!+(n-2)(n-2)!+…+2·2!+1·1!(n>1,且n∈N*)的结果时,第一步当n=____时,A=____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一个侧棱长为![]() 的直三棱柱
的直三棱柱![]() 容器中盛有液体(不计容器厚度).若液面恰好分别过棱
容器中盛有液体(不计容器厚度).若液面恰好分别过棱![]() 中点
中点![]() .
.
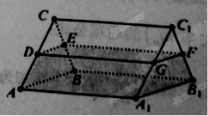
(1)求证:平面![]() 平面
平面![]() ;
;
(2)当底面![]() 水平放置时,求液面的高.
水平放置时,求液面的高.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等差数列{an}的公差不为零,首项a1=1,a2是a1和a5的等比中项,则数列的前10项之和是( )
A. 90 B. 100 C. 145 D. 190
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在建立两个变量Y与x的回归模型中,分别选择了4个不同模型,它们的相关指数R2如下,其中拟合得最好的模型是 ( )
A. 模型1的相关指数R2为0.98 B. 模型2的相关指数R2为0.80
C. 模型3的相关指数R2为0.50 D. 模型4的相关指数R2为0.25
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于①“一定发生的”,②“很可能发生的”,③“可能发生的”,④“不可能发生的”,⑤“不太可能发生的”这5种生活现象,发生的概率由小到大排列为(填序号)_________________。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com