
| 4-x2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:高中数学 来源: 题型:
| A、若m⊥l,n⊥l,则m∥n |
| B、若α⊥γ,β⊥γ,则α∥β |
| C、若m∥l,n∥l,则m∥n |
| D、若m∥α,n∥α,则m∥n |
查看答案和解析>>
科目:高中数学 来源: 题型:
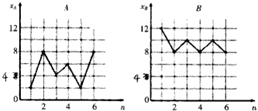 如图,样本A和B分别来自两个不同的总体,它们的样本平均数分别为
如图,样本A和B分别来自两个不同的总体,它们的样本平均数分别为. |
| xA |
. |
| xB |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
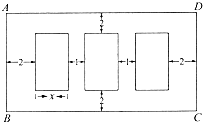 某公司因业务发展需要,准备印制如图所示的宣传彩页,宣传彩页有三幅大小相同的三个画面组成,每个画面的面积都是200cm2,这三个画面中都要绘制半径为5cm的圆形图案,为美观起见,每两个画面之间要留1cm的空白,三幅画周围要留2cm页边距,如图,设一边长x,所选用的彩页纸张面积为S
某公司因业务发展需要,准备印制如图所示的宣传彩页,宣传彩页有三幅大小相同的三个画面组成,每个画面的面积都是200cm2,这三个画面中都要绘制半径为5cm的圆形图案,为美观起见,每两个画面之间要留1cm的空白,三幅画周围要留2cm页边距,如图,设一边长x,所选用的彩页纸张面积为S查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com